
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() .
.
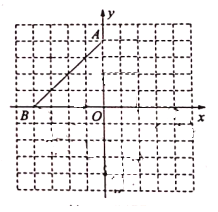
(1)①画出线段![]() 关于
关于![]() 轴对称的线段
轴对称的线段![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;
②将线段![]() 平移至
平移至![]() ,其中点
,其中点![]() 与点
与点![]() 对应,画出线段
对应,画出线段![]() 并写出点
并写出点![]() 的坐标;
的坐标;
(2)点![]() 在(1)中四边形
在(1)中四边形![]() 边
边![]() 上,且
上,且![]() 是对角线
是对角线![]() 上--动点,则
上--动点,则![]() 的最小值为 .
的最小值为 .
【答案】(1)①![]() ;②画出线段CD见解析,
;②画出线段CD见解析,![]() ;(2)6.
;(2)6.
【解析】
(1)①可知B和C是一组对应点,根据关于y轴对称的点横坐标互为相反数,纵坐标相同即可得出C点坐标同时画线段AC;②根据点![]() 与点
与点![]() 对应,确定平移方式,由点
对应,确定平移方式,由点![]() 与点
与点![]() 对应,即可写出D点坐标同时画出线段CD;
对应,即可写出D点坐标同时画出线段CD;
(2)根据B和C关于y轴对称,![]() 的最小值为线段BM,根据勾股定理求出BM即可.
的最小值为线段BM,根据勾股定理求出BM即可.
解:(1)①∵线段![]() 关于
关于![]() 轴对称的线段
轴对称的线段![]() ,
,![]() ,
,
∴![]() ,
,
线段![]() 见图1,
见图1,
故答案为:![]() ;
;
②∵点![]() 与点
与点![]() 对应,
对应,![]() ,
,![]() ,
,
∴平移方式为向下平移4单位,向右平移4单位,
∴![]() 的对应点D点的坐标为
的对应点D点的坐标为![]() ,
,
平移后的线段CD见图1:
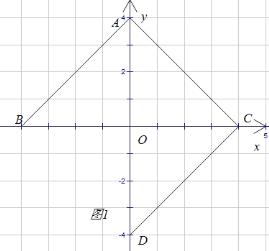
(2)如下图2,

在△BCD中,
∵![]() ,
,
∴![]() ,∠BDC=90°,
,∠BDC=90°,
∵B和C关于y轴对称,N在y轴上,
∴![]() ,
,
当B、M、N在同一条直线上时,![]() 最短为BM,
最短为BM,
此时![]() .
.
故答案为:6.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
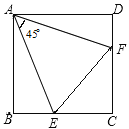
【题目】如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE、AF、EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数![]() ,导致了第一次数学危机.
,导致了第一次数学危机.![]() 是无理数的证明如下:
是无理数的证明如下:
假设![]() 是有理数,那么它可以表示成
是有理数,那么它可以表示成![]() (
(![]() 与
与![]() 是互质的两个正整数).于是
是互质的两个正整数).于是 ,所以,
,所以,![]() .于是
.于是![]() 是偶数,进而
是偶数,进而![]() 是偶数.从而可设
是偶数.从而可设![]() ,所以
,所以![]() ,
,![]() ,于是可得
,于是可得![]() 也是偶数.这与“
也是偶数.这与“![]() 与
与![]() 是互质的两个正整数”矛盾,从而可知“
是互质的两个正整数”矛盾,从而可知“![]() 是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,![]() 是无理数.这种证明“
是无理数.这种证明“![]() 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法B.反证法C.举反例法D.数学归纳法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,CE为△ABC的中线,BD为AC边上的高,BF平分∠CBD交CE于点G,连接AG交BD于点M,若∠AFG=63°,则∠AMB的度数为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子,并用线段表示;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学学习中,及时对知识进行归纳和整理是完善知识结构的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ .
(2)如果点C的坐标为(1,3) ,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠CAB交CD于F,CH⊥EF于H,连接DH,求证:(1)EH=FH;
(2)∠CAB=2∠CDH.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com