
如图,在平面直角坐标系xOy中,直线 与
与 轴交于点A(
轴交于点A(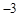 ,0),与
,0),与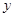 轴交于点B,且与直线
轴交于点B,且与直线 :
: 的交点为C(
的交点为C( ,4) .
,4) .
(1)求直线 的解析式;
的解析式;
(2)如果以点O,D,B,C为顶点的四边形是平行四边 形,直接写出点D的坐标;
(3)将直线 沿y轴向下平移3个单位长度得到直线
沿y轴向下平移3个单位长度得到直线 ,点P(m,n)为直线
,点P(m,n)为直线 上一动点,过点P作x轴的垂线, 分别与直线
上一动点,过点P作x轴的垂线, 分别与直线 ,
, 交于M,N.当点P在线段MN上时,请直接写出m的取值范围.
交于M,N.当点P在线段MN上时,请直接写出m的取值范围. 
(1)y= x+2;(2)点D的坐标是(3,2),(3,6)或(﹣3,﹣2);(3)﹣
x+2;(2)点D的坐标是(3,2),(3,6)或(﹣3,﹣2);(3)﹣ ≤m≤3
≤m≤3
解析试题分析:(1)把C(a,4)代入y=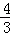 x求得a的值得出C的坐标,然后根据待定系数法即可求得直线l1的解析式;
x求得a的值得出C的坐标,然后根据待定系数法即可求得直线l1的解析式;
(2)过C点作OB的平行线,使BD=OB的点是D1(3,2),D2(3,6),过(3,6)作关于B点的中心对称点为D3(﹣3,﹣2);
(3)求得直线l3的解析式,然后求得与直线l2的交点,即可判断出m的取值;
试题解析:(1)∵直线l2:y=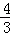 x经过点C(a,4),
x经过点C(a,4),
∴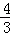 a=4,即a=3,
a=4,即a=3,
∴点C(3,4),
设直线l1的解析式为y=kx+b,
∵直线l1与x轴交于点A(﹣3,0),且经过点C(3,4),
∴将A与C代入得: ,
,
解得: ,
,
则直线l1的解析式为y= x+2;
x+2;
(2)∵B(0,2),C(3,4),
∴过C点作OB的平行线,使BD=OB的点是D1(3,2),D2(3,6),
过(3,6)作关于B点的中心对称点为D3(﹣3,﹣2),
∴点D的坐标是(3,2),(3,6)或(﹣3,﹣2);
(3)∵直线l1y= x+2向下平移3个单位,
x+2向下平移3个单位,
∴直线l3为:y= x﹣1,
x﹣1,
∵C(3,4),
∴直线l2为:y= x,
x,
解 得
得 ,
,
∴直线l2与直线l3的交点为(﹣ ,﹣2),
,﹣2),
∵直线l1与直线l2的交点为C(3,4),
∴﹣ ≤m≤3.
≤m≤3.
考点:一次函数综合题


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
如图,在以点O为原点的直角坐标系中,一次函数 的图象与x轴交于A、与y轴交于点B,点C在直线AB上,且OC=
的图象与x轴交于A、与y轴交于点B,点C在直线AB上,且OC= AB,反比例函数
AB,反比例函数 的图象经过点C,则所有可能的k值为 .
的图象经过点C,则所有可能的k值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
A城有肥料300吨,B城有肥料200吨,现要把这些肥料全部运往甲,乙两乡,从A城往甲,乙两乡运肥料的费用分别为每吨20元和25元;从B城往甲,乙两乡运肥料的费用分别为每吨25元和15元.现甲乡需要肥料260吨,乙乡需要肥料240吨.设从A城运往甲乡的肥料为x吨.
(1)请你填空完成下表中的每一空:
| 调入地 化肥量(吨) 调出地 | 甲乡 | 乙乡 | 总计 |
| A城 | x | _________ | 300 |
| B城 | _________ | _________ | 200 |
| 总计 | 260 | 240 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与x轴交于点A(1,0),与y轴交于点B(0,2),求一次函数y=kx+b的解析式及线段AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
直线 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与t之间的函数关系式(不要求写自变量的取值范围);
③点P(0,t)是y轴正半轴上的一个动点,为何值时点P、C、D恰好能组成一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知反比例函数y1= 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1<y2成立的自变量x的取值范围;
(3)在x轴的正半轴上存在一点P,且△ABP的面积是6,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y= 的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣ >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿折线BC﹣CD向点D运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F的运动时间为t秒.
(1)点F在边BC上.
①如图1,连接DE,AF,若DE⊥AF,求t的值;
②如图2,连结EF,DF,当t为何值时,△EBF与△DCF相似?
(2)如图3,若点G是边AD的中点,BG,EF相交于点O,试探究:是否存在在某一时刻t,使得 ?若存在,求出t的值;若不存在,请说明理由.
?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com