
直线 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与t之间的函数关系式(不要求写自变量的取值范围);
③点P(0,t)是y轴正半轴上的一个动点,为何值时点P、C、D恰好能组成一个等腰三角形?
(1)m=9;(2) ;(3)t=4,或t=
;(3)t=4,或t= ,t=
,t= 时,△PCD均为等腰三角形.
时,△PCD均为等腰三角形.
解析试题分析:(1)由直线的解析式可求出A和B点的坐标,再根据菱形的性质即可求出点C、点D的坐标,把点C的坐标代入直线y=x+m即可求出m的值;
(2)设点M的坐标为(xM,t),点N的坐标为(xN,t),首先求出xM=﹣ t+3,再求出xN=t﹣9,进而得到d=xM﹣xN=﹣
t+3,再求出xN=t﹣9,进而得到d=xM﹣xN=﹣ t+3﹣(t﹣9)=﹣
t+3﹣(t﹣9)=﹣ t+12;
t+12;
(3)由A和B的坐标可求出AB的长,再分三种情况分别讨论求出符合题意的t值即可.
试题解析:(1)∵直线y=﹣ x+4与x轴交于点A,与y轴交于点B,
x+4与x轴交于点A,与y轴交于点B,
∴点A的坐标为(3,0)点B的坐标为(0,4),
∵四边形ABCD是菱形,
∴点C的坐标为(﹣5,4),点D的坐标为(﹣2,0),
∵直线y=x+m经过点C,
∴m=9,
(2)∵MN 经过点P(0,t)且平行于x轴,
∴可设点M的坐标为(xM,t),点N的坐标为(xN,t),
∵点M在直线AB上,
直线AB的解析式为y=﹣ x+4,
x+4,
∴t= ,得xM=﹣
,得xM=﹣ t+3,
t+3,
同理点N在直线CE上,直线CE的解析式为y=x+9,
∴t=xN+9,得xN=t﹣9,
∵MN∥x轴且线段MN的长度为d,
∴d=xM﹣xN=﹣ t+3﹣(t﹣9)=﹣
t+3﹣(t﹣9)=﹣ t+12;
t+12;
(3)∵直线AB的解析式为y=﹣ x+4,
x+4,
∴点A 的坐标为(3,0),点B的坐标为(0,4),AB=5,
∵四边形ABCD是菱形,
∴AB=BC=CD=5,
∴点P运动到点B时,△PCD即为△BCD是一个等腰三角形,此时=4;
∵点P(0,t)是y轴正半轴上的一个动点,
∴OP=t,PB=|t﹣4|,
∵点D的坐标为(﹣2,0),
∴OD=2,由勾股定理得PD2=OD2+OP2=4+t2,
同理,CP2=BC2+BP2=25+(t﹣4)2,
当PD=CD=5时,PD2=4+t2=25,
∴t= (舍负),
(舍负),
当PD=CP时,PD2=CP2,4+t2=25+(t﹣4)2,
∴t= ,
,
综上所述,t=4,或t= ,t=
,t= 时,△PCD均为等腰三角形.
时,△PCD均为等腰三角形.
考点:一次函数综合题


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:填空题
五一节某超市搞促销活动:①一次性购物不超过150元不享受优惠;②一次性购物超过150元但不超过500元一律九折;③一次性购物超过500元一律八折.王宁两次购物分别付款120元、432元,若王宁一次性购买与上两次相同的商品,则应付款_________元.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
| 原料名称 饮料名称 | 甲 | 乙 |
| A | 20克 | 40克 |
| B | 30克 | 20克 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,直线 与
与 轴交于点A(
轴交于点A(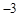 ,0),与
,0),与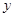 轴交于点B,且与直线
轴交于点B,且与直线 :
: 的交点为C(
的交点为C( ,4) .
,4) .
(1)求直线 的解析式;
的解析式;
(2)如果以点O,D,B,C为顶点的四边形是平行四边 形,直接写出点D的坐标;
(3)将直线 沿y轴向下平移3个单位长度得到直线
沿y轴向下平移3个单位长度得到直线 ,点P(m,n)为直线
,点P(m,n)为直线 上一动点,过点P作x轴的垂线, 分别与直线
上一动点,过点P作x轴的垂线, 分别与直线 ,
, 交于M,N.当点P在线段MN上时,请直接写出m的取值范围.
交于M,N.当点P在线段MN上时,请直接写出m的取值范围. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
(1)求⊙M的半径.
(2)求线段AC的长.
(3)若D为OA的中点,求证:CD是⊙M的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“五一黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的曲线表示.根据图象提供的有关信息,解答下列问题:
(1)小明全家在旅游景点游玩了多少小时?
(2)返程途中小汽车的速度每小时多少千米?请你求出来,并回答小明全家到家是什么时间?
(3)若出发时汽车油箱中存油15升,该汽车的油箱总容量为35升,汽车每行驶1千米耗油 升.
升.
请你就“何时加油和加油量”给小明全家提出一个合理化的建议.(加油所用时间忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某发电厂共有6台发电机发电,每台的发电量为300万千瓦/月.该厂计划从今年7月开始到年底,对6台发电机各进行一次改造升级.每月改造升级1台,这台发电机当月停机,并于次月再投入发电,每台发电机改造升级后,每月的发电量将比原来提高20%.已知每台发电机改造升级的费用为20万元.将今年7月份作为第1个月开始往后算,该厂第x(x是正整数)个月的发电量设为y(万千瓦).
(1)求该厂第2个月的发电量及今年下半年的总发电量;
(2)求y关于x的函数关系式;
(3)如果每发1千瓦电可以盈利0.04元,那么从第1个月开始,至少要到第几个月,这期间该厂的发电盈利扣除发电机改造升级费用后的盈利总额ω1(万元),将超过同样时间内发电机不作改造升级时的发电盈利总额ω2(万元)?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
设p,q都是实数,且 .我们规定:满足不等式
.我们规定:满足不等式 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为 .对于一个函数,如果它的自变量x与函数值y满足:当
.对于一个函数,如果它的自变量x与函数值y满足:当 时,有
时,有 ,我们就称此函数是闭区间
,我们就称此函数是闭区间 上的“闭函数”.
上的“闭函数”.
(1)反比例函数 是闭区间
是闭区间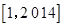 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间
是闭区间 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若实数c,d满足 ,且
,且 ,当二次函数
,当二次函数 是闭区间
是闭区间 上的“闭函数”时,求c,d的值.
上的“闭函数”时,求c,d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,已知直线l:y= x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 .
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com