
如图,已知直线AB与x轴、y轴分别交于A和B,OA=4,且OA、OB长是关于x的方程x2﹣mx+12=0的两实根,以OB为直径的⊙M与AB交于C,连接CM并延长交x轴于N.
(1)求⊙M的半径.
(2)求线段AC的长.
(3)若D为OA的中点,求证:CD是⊙M的切线.
(1)  ;(2)
;(2)  ;(3)证明见解析.
;(3)证明见解析.
解析试题分析:(1)由OA、OB长是关于x的方程x2﹣mx+12=0的两实根,得OA•OB=12,而OA=4,所以OB=3,又由于OB为⊙M的直径,即可得到⊙M的半径.
(2)连接OC,根据OB是⊙M直径,得到OC⊥BC,利用面积相等得到OC•AB=OA•OB可以求得OC的长,然后利用勾股定理求得AC的长即可.
(3)连MD,OC,由OB为⊙M的直径,得∠OCB=90°,则∠OCD=90°,由于D为OA的中点,所以CD= OA=OD,因此可证明△MCD≌△MOD,所以∠MCD=∠MOD=90°,即CD是⊙M的切线.
OA=OD,因此可证明△MCD≌△MOD,所以∠MCD=∠MOD=90°,即CD是⊙M的切线.
试题解析:(1)∵OA=4∴A(4,0)
又OA•OB长是x2﹣mx+12=0的两根
∴OA•OB=12∴OB=3 故B(0,3)
∵OB为直径
∴半径MB= ;
;
(2)连接OC
∵OB是⊙M直径
∴OC⊥BC
∴OC•AB=OA•OB
∵AB= ="5"
="5"
∴OC•5=3•4
∴OC=
∴AC=
(3)∵OM=MC∴∠MOC=∠MCO
又CD是Rt△OCA斜边上中线
∴DC=DO
∴∠DOC=∠DCO
∵∠DOC+∠MOC=90°
∴∠MCO+∠DCO=90°
∴DC⊥MC
∴CD是⊙M的切线
考点:一次函数综合题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:解答题
某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过20m3时,按2元/m3计算;月用水量超过20m3时,超过部分按2.6元/m3计费。设每户家庭用水量为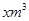 时,应交水费y元。
时,应交水费y元。
(1)分别求出 和
和 时y与x的关系式;
时y与x的关系式;
(2)小明家第二季度交纳水费的情况如下:
| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形OABC摆放在平面直角坐标系xOy中,点A在x轴上,点C在y轴上,OA=3,OC=2,P是BC边上一点且不与B重合,连结AP,过点P作∠CPD=∠APB,交x轴于点D,交y轴于点E,过点E作EF∥AP交x轴于点F.
(1)若△APD为等腰直角三角形,求点P的坐标;
(2)若以A,P,E,F为顶点的四边形是平行四边形,求直线PE的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
直线 与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
与x轴交于点A,与y轴交于点B,菱形ABCD如图放置在平面直角坐标系中,其中点D在x轴负半轴上,直线y=x+m经过点C,交x轴于点E.
①请直接写出点C、点D的坐标,并求出m的值;
②点P(0,t)是线段OB上的一个动点(点P不与O、B重合),经过点P且平行于x轴的直线交AB于M、交CE于N.设线段MN的长度为d,求d与t之间的函数关系式(不要求写自变量的取值范围);
③点P(0,t)是y轴正半轴上的一个动点,为何值时点P、C、D恰好能组成一个等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
画出函数y=﹣x+1的图象,结合图象,回答下列问题.
在函数y=﹣x+1的图象中:
(1)画出函数图象并写出与x轴的交点坐标是 _________ ;
(2)随着x的增大,y将 _________ (填“增大”或“减小”);
(3)当y取何值时,x<0? _________
(4)把它的图象向下平移2个单位长度则得到的新的一次函数解析式是 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,一次函数y=﹣x+2的图象与反比例函数y=﹣ 的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
的图象交于A、B两点,与x轴交于D点,且C、D两点关于y轴对称.
(1)求A、B两点的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数y=kx+b,当x=2时,y=﹣3,当x=1时,y=﹣1.
(1)求一次函数的解析式;
(2)若该一次函数的图形交x轴y轴分别于A、B两点,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
无论k取任何实数,对于直线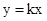 都会经过一个固定的点
都会经过一个固定的点 ,我们就称直线
,我们就称直线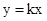 恒过定点
恒过定点 .
.
(1)无论 取任何实数,抛物线
取任何实数,抛物线 恒过定点
恒过定点 ,直接写出定点A的坐标;
,直接写出定点A的坐标;
(2)已知△ABC的一个顶点是(1)中的定点 ,且∠B,∠C的角平分线分别是y轴和直线
,且∠B,∠C的角平分线分别是y轴和直线 ,求边BC所在直线的表达式;
,求边BC所在直线的表达式;
(3)求△ABC内切圆的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com