
 ��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸���ABC�������������ߵĽ��㣩��
��ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У������˸���ABC�������������ߵĽ��㣩������ ��1�����������ص��ƽ�Ƶ����ʻ�����A��B��C�Ķ�Ӧ��A1��B1��C1���Ӷ��õ���A1B1C1��
��2�����������ص��λ�Ƶ�����������B��C�Ķ�Ӧ��B2��C2���Ӷ��õ���AB2C2��
��3���Ȱѵ�Aƽ�Ƶ���ԭ�㣬��M��ƽ�ƺ��Ӧ�������Ϊ��x-1��y-3������ʱ����λ�Ʊ任�ĵ��������ɵõ��任��M��Ķ�Ӧ�������Ϊ��3x-3��3y-9����Ȼ������ƽ�ưѵ㣨3x-3��3y-9��ƽ�Ƶ�ԭ����λ�õõ���3x-3+1��3y-9+3����
��� �⣺��1����ͼ����A1B1C1Ϊ������
��2����ͼ����AB2C2Ϊ������
��3��M�Ķ�Ӧ��M1������Ϊ��3x-2��3y-6����
�ʴ�Ϊ��3x-2��3y-6����
���� ���⿼������ͼ-λ�Ʊ任����ȷ��λ�����ģ��ֱ����Ӳ��ӳ�λ�����ĺ��ܴ���ԭͼ�Ĺؼ��㣬�ٸ���λ�Ʊȣ�ȷ���ܴ���������λ��ͼ�εĹؼ��㣬Ȼ��˳�������������㣬�õ��Ŵ����С��ͼ�Σ�Ҳ������ƽ�Ʊ任��


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����������������ᣬ�����������⣺
����������������ᣬ�����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
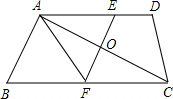 ��ͼ�����ı���ABCD�У�AD��BC��EF��ֱƽ��AC�ڵ�O���ֱ�AD��BC��E��F����֤��AE=AF��
��ͼ�����ı���ABCD�У�AD��BC��EF��ֱƽ��AC�ڵ�O���ֱ�AD��BC��E��F����֤��AE=AF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����B��E��C��F��ͬһֱ���ϣ�AB=DE����ABC=��DEF��BE=CF����֤��AC��DF��
��ͼ����B��E��C��F��ͬһֱ���ϣ�AB=DE����ABC=��DEF��BE=CF����֤��AC��DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
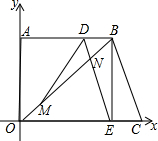 ��ͼ����ֱ������OABC�У���֪B��C���������ֱ�ΪB��8��6����C��10��0��������M��ԭ��O������OB���������˶����ٶ�Ϊ1��λ/�룻ͬʱ���߶�DE��BC������BA���������˶����ٶ�Ϊ1��λ/�룬��OB�ڵ�N������DM�����˶�ʱ��Ϊt�루0��t��8��
��ͼ����ֱ������OABC�У���֪B��C���������ֱ�ΪB��8��6����C��10��0��������M��ԭ��O������OB���������˶����ٶ�Ϊ1��λ/�룻ͬʱ���߶�DE��BC������BA���������˶����ٶ�Ϊ1��λ/�룬��OB�ڵ�N������DM�����˶�ʱ��Ϊt�루0��t��8���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com