(1)解:△DEC是等腰三角形,
理由是:∵AD∥BC,
∴∠A+∠B=180°,
∵∠A=90°,
∴∠B=90°=∠A,
在△ADE和△BEC中

∴△DAE≌△EBC,
∴DE=EC,
即△DEC是等腰三角形.

(2)∵AD=3,AB=7,△DAE≌△EBC,
∴AD=BE=3,AE=BC=7-3=4,∠ADE=∠BEC,
在Rt△AED中,由勾股定理得:DE=DC=5,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠BEC=90°,
∴∠DEC=180°-90°=90,
在Rt△DEC中,由勾股定理得:DC=

=
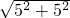
=5

.
分析:(1)求出∠A=∠B,证出△DAE≌△EBC,推出DE=EC即可;
(2)根据全等三角形性质得出AD=BE=3,AE=BC=7-3=4,∠ADE=∠BEC,在Rt△AED中,由勾股定理求出DE、CE,求出∠DEC=90°,根据勾股定理求出即可.
点评:本题考查了全等三角形的性质和判定和勾股定理,三角形的内角和定理的应用,主要考查学生的推理能力.

 如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠AED=∠ECB.
如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠AED=∠ECB.

 =
=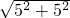 =5
=5 .
.
