
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.

(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
【答案】解:(1)∵四边形ABCD是正方形
∴∠A=∠B=∠D=90°,AD=AB
∵QE⊥AB,MF⊥BC
∴∠AEQ=∠MFB=90°
∴四边形ABFM、AEQD都是矩形
∴MF=AB,QE=AD,MF⊥QE
又∵PQ⊥MN
∴∠EQP=∠FMN
又∵∠QEP=∠MFN=90°
∴△PEQ≌△NFM.
(2)∵点P是边AB的中点,AB=2,DQ=AE=t
∴PA=1,PE=1-t,QE=2
由勾股定理,得PQ=![]() =
=![]()
∵△PEQ≌△NFM
∴MN=PQ=![]()
又∵PQ⊥MN
∴S=![]() =
=![]() =
=![]() t2-t+
t2-t+![]()
∵0≤t≤2
∴当t=1时,S最小值=2.
综上:S=![]() t2-t+
t2-t+![]() ,S的最小值为2.
,S的最小值为2.
【解析】试题分析:(1)由四边形ABCD是正方形得到∠A=∠B=∠D=90°,AD=AB,又由∠EQP=∠FMN,而证得;
(2)分为两种情况:①当E在AP上时,由点P是边AB的中点,AB=2,DQ=AE=t,又由勾股定理求得PQ,由△PEQ≌△NFM得到PQ的值,又PQ⊥MN求得面积S,由t范围得到S的最小值;②当E在BP上时,同法可求S的最小值.
试题解析:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠D=90°,AD=AB,
∵QE⊥AB,MF⊥BC,
∴∠AEQ=∠MFB=90°,
∴四边形ABFM、AEQD都是矩形,
∴MF=AB,QE=AD,MF⊥QE,
又∵PQ⊥MN,
∴∠1+∠EQP=90°,∠2+∠FMN=90°,
∵∠1=∠2,
∴∠EQP=∠FMN,
又∵∠QEP=∠MFN=90°,
∴△PEQ≌△NFM;
(2)分为两种情况:①当E在AP上时,
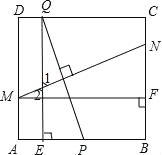
∵点P是边AB的中点,AB=2,DQ=AE=t,
∴PA=1,PE=1-t,QE=2,
由勾股定理,得PQ=![]() ,
,
∵△PEQ≌△NFM,
∴MN=PQ=![]() ,
,
又∵PQ⊥MN,
∴S=![]() t2-t+
t2-t+![]() ,
,
∵0≤t≤2,
∴当t=1时,S最小值=2.
②当E在BP上时,
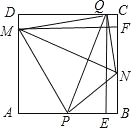
∵点P是边AB的中点,AB=2,DQ=AE=t,
∴PA=1,PE=t-1,QE=2,
由勾股定理,得PQ=![]() ,
,
∵△PEQ≌△NFM,
∴MN=PQ=![]() ,
,
又∵PQ⊥MN,
∴S=![]() t2-t+
t2-t+![]() ,
,
∵0≤t≤2,
∴当t=1时,S最小值=2.
综上:S=![]() t2-t+
t2-t+![]() ,S的最小值为2.
,S的最小值为2.


科目:初中数学 来源: 题型:
【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量 | 单价(元/m3) |
不超出80m3的部分 | 2.5 |
超出80m3不超出130m3的部分 | a |
超出130m3的部分 | a+0.5 |
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向.

(1)求∠CBA的度数;
(2)求出这段河的宽.(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
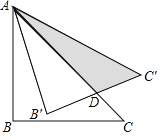
【题目】如图,等腰直角三角形ABC的直角边AB的长为![]() ,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于______.
,将△ABC绕点A逆时针旋转15°后得到△AB′C′,AC与B′C′相交于点D,则图中阴影△ADC′的面积等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b分别交x轴、y轴于A(1,0)、B(0,﹣1),交双曲线y=![]() 于点C、D.
于点C、D.
(1)求k、b的值;
(2)写出不等式kx+b>![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
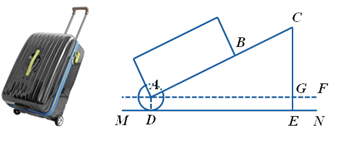
【题目】有一只拉杆式旅行箱(图1),其侧面示意图如图2所示.已知箱体长AB=50cm,拉杆![]() 的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
的伸长距离最大时可达35cm,点A,B,C在同一条直线上.在箱体底端装有圆形的滚轮⊙A,⊙A与水平地面MN相切于点D.在拉杆伸长至最大的情况下,当点B距离水平地面38cm时,点C到水平地面的距离CE为59cm.
设AF∥MN.
(1)求⊙A的半径长;
(2)当人的手自然下垂拉旅行箱时,人感到较为舒服.某人将手自然下垂在C端拉旅行箱时,CE为80cm,![]() =64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:
=64°.求此时拉杆BC的伸长距离.(精确到1cm,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
(1)若点A1的坐标为(2,1),则点A4的坐标为_____;
(2)若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图1,抛物线y=﹣![]() x2﹣
x2﹣![]() x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC
x+3与x轴交于A和B两点(点A在点B的左侧),与y轴相交于点C,点D的坐标是(0,﹣1),连接BC、AC

(1)求出直线AD的解析式;
(2)如图2,若在直线AC上方的抛物线上有一点F,当△ADF的面积最大时,有一线段MN=![]() (点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(点M在点N的左侧)在直线BD上移动,首尾顺次连接点A、M、N、F构成四边形AMNF,请求出四边形AMNF的周长最小时点N的横坐标;
(3)如图3,将△DBC绕点D逆时针旋转α°(0<α°<180°),记旋转中的△DBC为△DB′C′,若直线B′C′与直线AC交于点P,直线B′C′与直线DC交于点Q,当△CPQ是等腰三角形时,求CP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com