
【题目】如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸边点A处,测得河的北岸点B在其北偏东45°方向,然后向西走60m到达C点,测得点B在点C的北偏东60°方向.

(1)求∠CBA的度数;
(2)求出这段河的宽.(结果精确到1m,备用数据 ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】新能源汽车投放市场后,有效改善了城市空气质量。经过市场调查得知,某市去年新能源汽车总量已达到3250辆,预计明年会增长到6370辆.
(1)求今、明两年新能源汽车数量的平均增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对今年增加的新能源汽车给予每辆0.8万元的政府性补贴.在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 2.将△ABC绕顶点C逆时针旋转得到△![]() 使点
使点![]() 落在AC边上.设M是
落在AC边上.设M是![]() 的中点,连接BM,CM,则△BCM的面积为( )
的中点,连接BM,CM,则△BCM的面积为( )
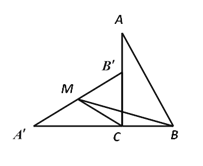
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
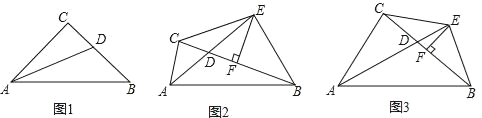
【题目】在△ABC,∠BAC为锐角,AB>AC,AD平分∠BAC交BC于点D.
(1)如图1,若△ABC是等腰直角三角形,直接写出线段AC,CD,AB之间的数量关系;
(2)BC的垂直平分线交AD延长线于点E,交BC于点F.
①如图2,若∠ABE=60°,判断AC,CE,AB之间有怎样的数量关系并加以证明;
②如图3,若AC+AB=![]() AE,求∠BAC的度数.
AE,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,|x|表示x在数轴上对应的点到原点的距离,我们可以把看作|x-0|,所以,|x- 3|就表示x在数轴上对应的点到3的距离,|x1||x-(-1)|就表示x在数轴上对应的点到-1的距离,由上面绝对值的几意义,解答下列问题:
(1) 当|x-4||x2|有最小值时,x的取值情况是 ;
(2) |x-3||x2 ||x6|的最小值是 ;
(3) 已知| x -1||x2 ||y-3||y4|10 求2xy 的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图是指用无刻度的直尺和圆规作图。尺规作图是起源于古希腊的数学课题.只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题.初中阶段同学们首次接触的尺规作图是“作一条线段等于已知线段”.

图1

图2
![]()
备用图
(1)如图1,在线段![]() 外有一点
外有一点![]() ,现在利用尺规作图验证“两点之间线段最短”,
,现在利用尺规作图验证“两点之间线段最短”,![]() .请根据提示,用尺规完成作图,并补充验证步骤.
.请根据提示,用尺规完成作图,并补充验证步骤.
第一步,以![]() 为圆心,
为圆心,![]() 为半径作弧,交线段
为半径作弧,交线段![]() 于点
于点![]() ,则
,则![]() _____________;
_____________;
第二步,以![]() 为圆心,
为圆心,![]() 为半径作弧,交线段
为半径作弧,交线段![]() 于点
于点![]() ,则
,则![]() _____________;
_____________;
则![]() ______________
______________![]() _______________
_______________![]()
![]() _______________
_______________
故:![]() .
.
(2)如图2,在直线![]() 上,从左往右依次有四个点
上,从左往右依次有四个点![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .现以
.现以![]() 为圆心,半径长为
为圆心,半径长为![]() 作圆,与直线
作圆,与直线![]() 两个交点中右侧交点记为点
两个交点中右侧交点记为点![]() .再以
.再以![]() 为圆心;相同半径长
为圆心;相同半径长![]() 作圆,与直线
作圆,与直线![]() 两个交点中左侧交点记为点
两个交点中左侧交点记为点![]() .若
.若![]() ,
,![]() ,
,![]() 三点中,有一点分另外两点所连线段之比为
三点中,有一点分另外两点所连线段之比为![]() ,求半径
,求半径![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.

(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com