
����Ŀ��ijũ��Ʒ���������ջ����192�֣����˸��ס������صijа��̽��а������û����ô�С���ֻ�����18��ǡ����һ��������������������֪�����ֻ������������ֱ�Ϊ14��/�ֺ�8��/���������ס������ص��˷����±���
���� | �˷� | |
������/��Ԫ/���� | �����ҵ�/��Ԫ/���� | |
����� | 720 | 800 |
���� | 500 | 650 |
��1���������ֻ������ö�������
��2���������10������ǰ���أ��������ǰ���ҵأ�����ǰ���صĴ����Ϊa�������˷�ΪwԪ����w����a�ĺ�����ϵʽ��
��2���ڣ�2���������£����صijа��̰����ĺ���������96�֣�������Ƴ�ʹ���˷���͵Ļ������䷽���������������˷ѣ�
���𰸡���1���������8����С������10������2��w=70a+11400��0��a��8��Ϊ����������3��ʹ���˷����ٵĵ��䷽���ǣ�3���������7��С����ǰ���أ�5���������3��С����ǰ���ҵأ������˷�Ϊ11610Ԫ��
����������������1�����ݴ�С���ֻ�����18�����Լ����ֳ����˵Ļ���ĺ���192�����ݴ˼����з��̻��鼴�������
��2�����ȱ�ʾ��ÿ�ֳ�����ÿ��·���еķ��������˷�ΪwԪ���Ǹ������õĺ����ݴ˼���д��������ϵʽ��
��3�����������ص����ʲ�����96���������г�����ʽ���a�ķ�Χ���ٸ���a������������ȷ��a��ֵ�����ݣ�2���еĺ�����ϵ������ȷ��w����Сֵ��ȷ�����䷽����
�������1����������x������С�����ã�18��x�����������������
14x+8��18��x��=192�������x=8��18��x=18��8=10��
�����������8����������10����
��2���������صĴ������a����ô�����ҵصĴ������Ӧ���ǣ�8��a���������ص�С�����ǣ�10��a���������ҵص�С������10����10��a����w=720a+800��8��a��+500��10��a��+650[10����10��a��]=70a+11400��0��a��8��Ϊ��������
��3��14a+8��10��a����96�������a��![]() ���֡�0��a��8����3��a��8 ��Ϊ������
���֡�0��a��8����3��a��8 ��Ϊ������
��w=70a+11400��k=70��0��w��a��������������൱a=3ʱ��W��С����СֵΪ��W=70��3+11400=11610��Ԫ����
����ʹ���˷����ٵĵ��䷽������3���������7��С����ǰ������5���������3��С����ǰ���ҵأ������˷�Ϊ11610Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥AB��16�ף�Զ����һ��CD��ij����¥��B���������������Ϊ38.5�㣬����¥��A���������������Ϊ22�㣬������CD����¥����֮��ľ���BD�ij������ο����ݣ�sin22���0.37��cos22���0.93��tan22���0.40��sin38.5���0.62��cos38.5���0.78��tan38.5���0.80 ��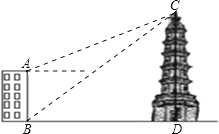
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��
��![]() ��
��![]() ���������������ֱ���
���������������ֱ���![]() ��
��![]() ��
��![]() ����
����![]() ��������ѡ���У���һ����ʾ
��������ѡ���У���һ����ʾ![]() ��
��![]() ��
��![]() �����������ϵ�λ�ù�ϵ�����ѡ��Ϊ�Σ��� ��
�����������ϵ�λ�ù�ϵ�����ѡ��Ϊ�Σ��� ��
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ɱ߳�Ϊ1��С��������ɵ������У�������ABC�Ķ�������ڸ���ϣ�
��1������ABC�Ƶ�O˳ʱ����ת90��õ���A1B1C1 �� �������л�����A1B1C1��
��2�����߶�OA����ת������ɨ����ͼ�����������������У�
��3�����BCC1������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻ�����ͯ��ҵ�����ij����Ҫ����ͼ�е�AB���ڵ�ֱ���Ͻ�һͼ���ң�������������ѧУ���ڵ�λ���ڵ�C�͵�D����CA��AB��A��DB��AB��B.��֪AB=2.5km��CA=1.5km��DB=1.Okm�����ʣ�ͼ����EӦ�ý��ھ��A����km��������ʹ��������ѧУ�ľ�����ȣ�
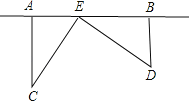
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С�ƴӶ��κ���y=ax2+bx+c��a��0����ͼ���еõ�������Ϣ��
��ab��0
��4a+b=0
�۵�y=5ʱֻ�ܵ�x=0
�ܹ���x��һԪ���η���ax2+bx+c=10����������ȵ�ʵ������
����Ϊ������ȷ���У� ��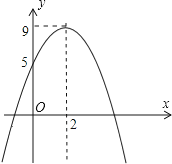
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ![]() ��һ����Ϊ
��һ����Ϊ![]() ����Ϊ
����Ϊ![]() �ij����Σ�����
�ij���������![]() ��
��![]() ����������
��Ϊ��������![]() ������ͼ�������ü������ȷֳ��Ŀ���ͬС�����Σ�Ȼ��ͼ
������ͼ�������ü������ȷֳ��Ŀ���ͬС�����Σ�Ȼ��ͼ![]() ��ʽƴ��һ���������Σ�
��ʽƴ��һ���������Σ�
��ͼ![]() ��һ����Ϊ
��һ����Ϊ![]() ����Ϊ
����Ϊ![]() �ij����Σ�����
�ij���������![]() ��
��![]() ����������
��Ϊ��������![]() ������ͼ�������ü������ȷֳ��Ŀ���ͬС�����Σ�Ȼ��ͼ
������ͼ�������ü������ȷֳ��Ŀ���ͬС�����Σ�Ȼ��ͼ![]() ��ʽƴ��һ���������Σ�
��ʽƴ��һ���������Σ�
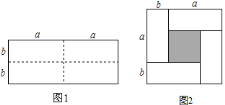
![]() ����Ϊͼ
����Ϊͼ![]() �д������εı߳�Ϊ________��С�����Σ���Ӱ���֣��ı߳�Ϊ________�����ú�
�д������εı߳�Ϊ________��С�����Σ���Ӱ���֣��ı߳�Ϊ________�����ú�![]() ��
��![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
![]() ��ϸ�۲�ͼ
��ϸ�۲�ͼ![]() ������д��������������ʽ��
������д��������������ʽ��![]() ��
��![]() ��
��![]() ����ʾ��ͼ�����֮�����ȹ�ϵ����ѡȡ�ʺ�
����ʾ��ͼ�����֮�����ȹ�ϵ����ѡȡ�ʺ�![]() ��
��![]() ����ֵ������֤��
����ֵ������֤��
![]() ��֪
��֪![]() ��
��![]() �������ʽ
�������ʽ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ���̣��ڹ����б�ʱ���ӵ��ס����������̶ӵ�Ͷ���飮ʩ��һ�죬�踶���̶ӹ��̿�1.2��Ԫ���ҹ��̶ӹ��̿�0.5��Ԫ�������쵼С����ݼס������ӵ�Ͷ������㣬�����·�����
��1���ӵ����������̸պ�������ɣ�
��2���Ҷӵ�����������Ҫ�ȹ涨���ڶ���6�죻
��3�����ס������Ӻ���3�죬���µĹ������Ҷӵ�����Ҳ����������ɣ�
���ʣ�(1)�涨�����Ƕ����죿
(2)�ڲ������ڵ�ǰ���£��������һ��ʩ���������ʡ���̿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ���һ�������Թ�¥Ϊ�������ڶ�������Ӫ�ˣ���Ϊ��������Ϊ�����г���̣���λ��![]() �����Ⱥ�����¼���£�
�����Ⱥ�����¼���£�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() �����һ���˿��͵�Ŀ�ĵأ�������¥�������Զ���ڹ�¥��ʲô����
�����һ���˿��͵�Ŀ�ĵأ�������¥�������Զ���ڹ�¥��ʲô����
![]() �������ʻ�����У����¥��Զ�ľ����Ƕ��٣�
�������ʻ�����У����¥��Զ�ľ����Ƕ��٣�
![]() �������۲��Ź涨���ۣ�������
�������۲��Ź涨���ۣ�������![]() ǧ�ף�Ϊ
ǧ�ף�Ϊ![]() Ԫ������
Ԫ������![]() ǧ�IJ���ÿǧ�ļ۸�Ϊ
ǧ�IJ���ÿǧ�ļ۸�Ϊ![]() Ԫ��˾��һ�������Ӫҵ���Ƕ��٣�
Ԫ��˾��һ�������Ӫҵ���Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com