
分析 根据题目中的数据可以解答本题.
解答 解:在-1$\frac{1}{3}$,20%,$\frac{22}{7}$,0.3,0,3.14,-1.7,21,-2,1.01001 …,+6,π中,
正数集合是{20%,$\frac{22}{7}$,0.3,3.14,21,1.01001 …,+6,π},
负数集合是{$-1\frac{1}{3}$,-1.7,-2},
非负整数集合是{0,21,6},
分数集合是{$-1\frac{1}{3}$,20%,$\frac{22}{7}$,0.3,3.14,-1.7},
有理数集合是{-1$\frac{1}{3}$,20%,$\frac{22}{7}$,0.3,0,3.14,-1.7,21,-2,+6},
无理数集合是{1.01001 …,+6},
故答案为:(1)20%,$\frac{22}{7}$,0.3,3.14,21,1.01001 …,+6,π;
(2)$-1\frac{1}{3}$,-1.7,-2;
(3)0,21,6;
(4)$-1\frac{1}{3}$,20%,$\frac{22}{7}$,0.3,3.14,-1.7;
(5)-1$\frac{1}{3}$,20%,$\frac{22}{7}$,0.3,0,3.14,-1.7,21,-2,+6;
(6)1.01001 …,+6.
点评 本题考查实数,解题的关键是明确实数的划分方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
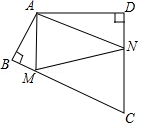 如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为140°.
如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为140°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
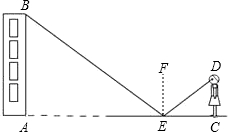 小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.
小红用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面点E处放一面平面镜,镜子与教学大楼的距离AE=20m.当她与镜子的距离CE=2.5m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.5m,请你帮助小红计算大楼的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com