
分析 (1)甲方式购买和包装x吨农产品所需资金为:4x万元;乙方式购买和加工其余农产品所需资金为:3(20-x)+3(20-x)+12=(132-6x)万元;
(2)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入-经营总成本=wA+wB-3×20;②由①中的函数解析式根据二次函数性质和一次函数的性质可得答案.
解答 解:(1)甲方式购买和包装x吨农产品所需资金为:4x万元;
乙方式购买和加工其余农产品所需资金为:3(20-x)+3(20-x)+12=(132-6x)万元;
故答案为:4x,(132-6x);
(2)1)当2≤x<8时,
w甲=x(-x+14)-x=-x2+13x;
w乙=9(20-x)-[12+3(20-x)]=108-6x
∴w=w甲+w乙-3×20
=(-x2+13x)+(108-6x)-60
=-x2+7x+48;
当x≥8时,
w甲=6x-x=5x;
w乙=9(20-x)-[12+3(20-x)]=108-6x
∴w=w甲+w乙-3×20
=(5x)+(108-6x)-60
=-x+48.
2)∵当2≤x<8时,w=-x2+7x+48=-(x-3.5)2+60.25,
∴当x=8时,w最小=40;
当x≥8时,w=-x+48中w随x的增大而减小,
∴当x=8时,w最小=40,
故当x=8时,利润最小为40万元.
点评 本题考查了二次函数、一次函数的综合应用题,解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.


科目:初中数学 来源: 题型:填空题
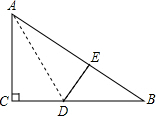 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,将纸片沿AD折叠,直角边AC恰好落在斜边上,且与AE重合,则△BDE的面积为6cm2.
如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,将纸片沿AD折叠,直角边AC恰好落在斜边上,且与AE重合,则△BDE的面积为6cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{25}{8}$ | B. | $\frac{25}{16}$ | C. | $\frac{25}{4}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
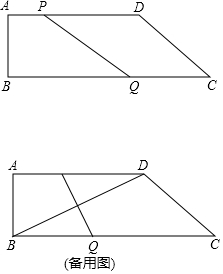 如图,在四边形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个端点也随之停止运动.
如图,在四边形ABCD中,AD‖BC,∠B=90°,AB=4cm,AD=8cm,BC=14cm,点P从点A出发,以1cm/s的速度向点D运动;点Q从点C同时出发,以3cm/s的速度向点B运动,规定其中一个动点到达端点时,另一个端点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一运动员推铅球,铅球经过的路线为如图所示的抛物线.
一运动员推铅球,铅球经过的路线为如图所示的抛物线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com