
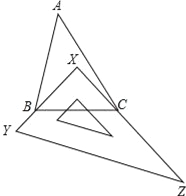
【题目】如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角板的位置,但仍使点B,点C在三角板的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
【答案】(1)60°;(2)∠ABX+∠ACX的大小没有变化;理由见解析.
【解析】试题分析:(1)在△ABC中,利用三角形内角和得出∠ABC+∠ACB=180°﹣∠A,即可求∠ABC+∠ACB;同理在△XBC中,∠BXC=90°,那么∠XBC+∠XCB=90°,即可得出结果;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A是一个定值,同理在△XBC中,∠BXC=90°,∠XBC+∠XCB=90°也是一个定值,∠ABX+∠ACX=90°﹣∠A的值不变.
试题解析:(1)∵∠A=30°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣30°=150°,
∵∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=150°﹣90°=60°;
(2)∠ABX+∠ACX的大小没有变化.理由如下:
∵∠ABC+∠ACB=180°﹣∠A,∠YXZ=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=180°﹣∠A﹣90°=90°﹣∠A;
即∠ABX+∠ACX的大小没有变化.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是半径为10的圆O所在平面上的一点,且点P到点O的距离为8.则过点P的直线l与圆O的位置关系为( )
A. 相交B. 相切
C. 相离D. 相交、相切、相离都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,①三角形的内角中最多有一个钝角;②三角形的中线将三角形分成面积相等的两部分;③从n边形的一个顶点可以引(n-3)条对角线,把n边形分成(n-2)个三角形,因此,n边形的内角和是(n-2)180°;④六边形的对角线有7条,正确的个数有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:y﹣3与x成正比例,且当x=﹣2时,y的值为7.
(1)求y与x之间的函数关系式;
(2)若点(﹣2,m)、点(4,n)是该函数图象上两点,比较m、n的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com