
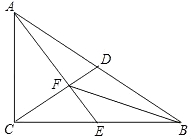
【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.

【答案】略
【解析】
试题分析:(1)先根据题意得出△ACB∽△ECA,再由直角三角形的性质得出CD=AD,由∠CAD+∠ABC=90°可得出∠ACD+∠EAC=90°,进而可得出∠AFC=90°;
(2)根据AE⊥CD可得出∠EFC=90°,∠ACE=∠EFC,故可得出△ECF∽△EAC,再由点E是BC的中点可知CE=BE,故![]() ,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
,根据∠BEF=∠AEB得出△BEF∽△AEB,进而可得出结论.
试题解析:(1)∵AC2=CECB,
∴![]() .
.
又∵∠ACB=∠ECA=90°
∴△ACB∽△ECA,
∴∠ABC=∠EAC.
∵点D是AB的中点,
∴CD=AD,
∴∠ACD=∠CAD
∵∠CAD+∠ABC=90°,
∴∠ACD+∠EAC=90°
∴∠AFC=90°,
∴AE⊥CD
(2)∵AE⊥CD,
∴∠EFC=90°,
∴∠ACE=∠EFC
又∵∠AEC=∠CEF,
∴△ECF∽△EAC
∴![]()
∵点E是BC的中点,
∴CE=BE,
∴![]()
∵∠BEF=∠AEB,
∴△BEF∽△AEB
∴∠EBF=∠EAB.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】【问题学习】小芸在小组学习时问小娟这样一个问题:已知α为锐角,且sinα=![]() ,求sin2α的值.小娟是这样给小芸讲解的:
,求sin2α的值.小娟是这样给小芸讲解的:
构造如图1所示的图形,在⊙O中,AB是直径,点C在⊙O上,所以∠ACB=90°,作CD⊥AB于D.设∠BAC=α,则sinα=![]() ,可设BC=x,则AB=3x,….
,可设BC=x,则AB=3x,….
【问题解决】
(1)请按照小娟的思路,利用图1求出sin2α的值;(写出完整的解答过程)
(2)如图2,已知点M,N,P为⊙O上的三点,且∠P=β,sinβ=![]() ,求sin2β的值.
,求sin2β的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
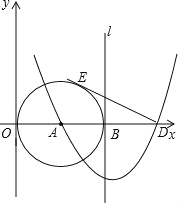
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a=﹣0.32,b=﹣3﹣2,c=![]() ;d=
;d=![]() ,则它们的大小关系是( )
,则它们的大小关系是( )
A. a<b<c<d B. b<a<d<c C. a<d<c<b D. c<a<d<b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国倡导的“一带一路”建设将促进世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为44亿人,这个数用科学记数法表示为( )
A. 44×108B. 4.4×108C. 4.4×1010D. 4.4×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一副三角板ABC和DEF中.
(1)当AB∥CD,如图①,求∠DCB的度数. 
(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由.
(3)如图③,当∠DCB等于多少度时,AB∥EC?
查看答案和解析>>
科目:初中数学 来源: 题型:
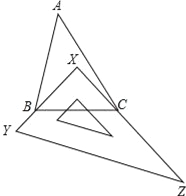
【题目】如图所示,有一块直角三角板XYZ放置在△ABC中,三角板的两条直角边XY和XZ恰好分别经过点B和点C.
(1)若∠A=30°,则∠ABX+∠ACX的大小是多少?
(2)若改变三角板的位置,但仍使点B,点C在三角板的边XY和边XZ上,此时∠ABX+∠ACX的大小有变化吗?请说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com