
【题目】在一副三角板ABC和DEF中.
(1)当AB∥CD,如图①,求∠DCB的度数. 
(2)当CD与CB重合时,如图②,判定DE与AC的位置关系,并说明理由.
(3)如图③,当∠DCB等于多少度时,AB∥EC?
【答案】
(1)解:∵AB∥CD,
∴∠DCB=∠ABC=30°
(2)解:DE∥AC.理由如下:
∵∠CDE=∠ACB=90°,
∴DE⊥CD,AC⊥BC,
∵CD与CB重合,
∴DE⊥BC,AC⊥BC,
∴DE∥AC
(3)解:∵AB∥EC,
∴∠ABC=∠BCE=30°,
又∵∠DCE=45°,
∴∠DCB=∠DCE﹣∠BCE=15°.
故当∠DCB等于15度时,AB∥EC
【解析】(1)根据“两直线平行,内错角相等”结合三角板角的特点即可得出结论;(2)根据三角板角的特点可得出DE⊥CD,AC⊥BC,再根据“垂直于同一直线的两直线平行”即可得出结论;(3)根据“两直线平行,内错角相等”即可得出∠ABC=∠BCE,再根据三角板角的特点通过角的计算即可得出结论.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
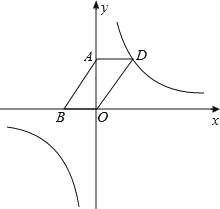
【题目】已知反比例函数y=![]() (m为常数)的图象在一、三象限.
(m为常数)的图象在一、三象限.
(1)求m的取值范围;
(2)如图,若该反比例函数的图象经过ABOD的顶点D,点A、B的坐标分别为(0,3),(﹣2,0).
①求出函数解析式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为 ;若以D、O、P为顶点的三角形是等腰三角形,则满足条件的点P的个数为 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合运用:
(1)已知![]() ,求a2+
,求a2+![]() 的值.
的值.
(2)已知a是4+![]() 的小数部分,b是﹣
的小数部分,b是﹣![]() +5的小数部分,c是(﹣
+5的小数部分,c是(﹣![]() +2)﹣1的整数部分,求a2c﹣b2c的值.
+2)﹣1的整数部分,求a2c﹣b2c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从小华家到姥姥家,有一段上坡路和一段下坡路.星期天,小华骑自行车去姥姥家,如果保持上坡每小时行3km,下坡每小时行5km,他到姥姥家需要行66分钟,从姥姥家回来时需要行78分钟才能到家.那么,从小华家到姥姥家上坡路和下坡路各有多少千米,姥姥家离小华家有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校学生的每日运动量,收集数据正确的是( )
A.调查该校舞蹈队学生每日的运动量
B.调查该校书法小组学生每日的运动量
C.调查该校田径队学生每日的运动量
D.调查该校某一班级的学生每日的运动量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是半径为10的圆O所在平面上的一点,且点P到点O的距离为8.则过点P的直线l与圆O的位置关系为( )
A. 相交B. 相切
C. 相离D. 相交、相切、相离都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:y﹣3与x成正比例,且当x=﹣2时,y的值为7.
(1)求y与x之间的函数关系式;
(2)若点(﹣2,m)、点(4,n)是该函数图象上两点,比较m、n的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com