
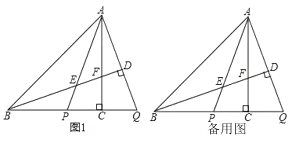
【题目】如图,在等腰直角△ABC中,∠ACB=90点P在线段BC上,延长BC至点Q,使得CQ=CP,连接AP,AQ.过点B作BD⊥AQ于点D,交AP于点E,交AC于点F.K是线段AD上的一个动点(与点A,D不重合),过点K作GN⊥AP于点H,交AB于点G,交AC于点M,交FD的延长线于点N.
(1)依题意补全图1;
(2)求证:NM=NF;
(3)若AM=CP,用等式表示线段AE,GN与BN之间的数量关系,并证明.
【答案】(1)见解析;(2)见解析;(3)BN=AE+GN,见解析.
【解析】
(1)根据题意补全图1即可;
(2)根据等腰三角形的性质得到AP=AQ,求得∠APQ=∠Q,求得∠MFN=∠Q,同理,∠NMF=∠APQ,等量代换得到∠MFN=∠FMN,于是得到结论;
(3)连接CE,根据线段垂直平分线的性质得到AP=AQ,求得∠PAC=∠QAC,得到∠CAQ=∠QBD,根据全等三角形的性质得到CP=CF,求得AM=CF,得到AE=BE,推出直线CE垂直平分AB,得到∠ECB=∠ECA=45°,根据全等三角形的性质即可得到结论.
(1)依题意补全图1如图所示;

(2)∵CQ=CP,∠ACB=90°,
∴AP=AQ,
∴∠APQ=∠Q,
∵BD⊥AQ,
∴∠QBD+∠Q=∠QBD+∠BFC=90°,
∴∠Q=∠BFC,
∵∠MFN=∠BFC,
∴∠MFN=∠Q,
同理,∠NMF=∠APQ,
∴∠MFN=∠FMN,
∴NM=NF;
(3)连接CE,
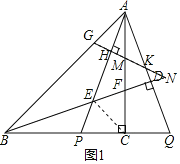
∵AC⊥PQ,PC=CQ,
∴AP=AQ,
∴∠PAC=∠QAC,
∵BD⊥AQ,
∴∠DBQ+∠Q=90°,
∵∠Q+∠CAQ=90°,
∴∠CAQ=∠QBD,
∴∠PAC=∠FBC,
∵AC=BC,∠ACP=∠BCF,
∴△APC≌△BFC(AAS),
∴CP=CF,
∵AM=CP,
∴AM=CF,
∵∠CAB=∠CBA=45°,
∴∠EAB=∠EBA,
∴AE=BE,
∵AC=BC,
∴直线CE垂直平分AB,
∴∠ECB=∠ECA=45°,
∴∠GAM=∠ECF=45°,
∵∠AMG=∠CFE,
∴△AGM≌△CEF(ASA),
∴GM=EF,
∵BN=BE+EF+FN=AE+GM+MN,
∴BN=AE+GN.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了解高校学生对5G移动通信网络的消费意愿,从在校大学生中随机抽取了1000人进行调查,下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图(例如,早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%).
用户分类 | 人数 |
A:早期体验用户(目前已升级为5G用户) | 260人 |
B:中期跟随用户(一年内将升级为5G用户) | 540人 |
C:后期用户(一年后才升级为5G用户) | 200人 |
下列推断中,不合理的是( )

A.早期体验用户中,愿意为5G套餐多支付10元,20元,30元的人数依次递减
B.后期用户中,愿意为5G套餐多支付20元的人数最多
C.愿意为5G套餐多支付10元的用户中,中期跟随用户人数最多
D.愿意为5G套餐多支付20元的用户中,后期用户人数最多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2+PB2=PC2,则称点P为△ABC关于点C的勾股点.

(1)如图2,在4×3的方格纸中,每个小正方形的边长均为1,△ABC的顶点在格点上,请找出所有的格点P,使点P为△ABC关于点A的勾股点.
(2)如图3,△ABC为等腰直角三角形,P是斜边BC延长线上一点,连接AP,以AP为直角边作等腰直角三角形APD(点A、P、D顺时针排列)∠PAD=90°,连接DC,DB,求证:点P为△BDC关于点D的勾股点.
(3)如图4,点E是矩形ABCD外一点,且点C是△ABE关于点A的勾股点,若AD=8,CE=5,AD=DE,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运用语音识别输入统计可以提高文字输入的速度,为了解A,B两种语音识别输入软件的可读性,小秦同学随机选择了20段话,其中每段话都含有100个字(不计标点符号),在保持相同条件下,标准普通话来测试两种语音识别输入软件的准确性,整个测试分析过程如下,请补充完整.
(1)收集数据:两种软件每次识别正确的字数记录如下:

(2)整理,描述数据:根据上面得到的两组样本数据,绘制了分布直方图
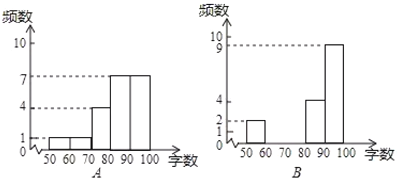
(3)分析数据:两组样本数据的平均数,众数,中位数,方差如下表所示
平均数 | 众数 | 中位数 | 方差 | |
A | 84.7 | 84.5 | 88.91 | |
B | 83.7 | 96 | 184.01 |
(4)得出结论:根据以上信息.判断____种语音识别输入软件的准确性较好,理由如下._______________(至少从两个不同的角度说明判断的合理性) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿折线
的速度沿折线![]() 运动,点
运动,点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 运动,
运动,![]() ,
,![]() 两点同时出发,当某一点运动到点
两点同时出发,当某一点运动到点![]() 时,两点同时停止运动.设运动时间为
时,两点同时停止运动.设运动时间为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 关于
关于![]() 的函数图像由
的函数图像由![]() ,
,![]() 两段组成,如图2所示.
两段组成,如图2所示.
(1)求![]() 的值;
的值;
(2)求图2中图像![]() 段的函数表达式;
段的函数表达式;
(3)当点![]() 运动到线段
运动到线段![]() 上某一段时
上某一段时![]() 的面积,大于当点
的面积,大于当点![]() 在线段
在线段![]() 上任意一点时
上任意一点时![]() 的面积,求
的面积,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,阿里巴巴“爱心助农”计划全面启动,集合天猫、淘宝、聚划算、饿了么、盒马、阿里乡村事业部等,组成了线上线下农产品销售的全域网络,通过这次爱心助农,很多农产品从滞销转变为脱销,以下是某淘宝商家在电商平台上推出的![]() .猕猴桃、
.猕猴桃、![]() .芒果这两种水果,其销售信息如下表:
.芒果这两种水果,其销售信息如下表:
品种 | 销售信息 |
| 5所以内(包含5斤),每斤8元;超过5斤,则超出部分打8折 |
| 3斤以内(包含3斤),每斤10元;超出3斤,所有芒果打9折 |
(1)小佳购买![]() 斤猕猴桃,付款
斤猕猴桃,付款![]() 元,请写出
元,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若小佳购买10斤猕猴桃,小欣购买8斤芒果,比较谁的花费更低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班甲、乙、丙三名同学20天的体温数据记录如下表:
甲的体温 | 乙的体温 | 丙的体温 | ||||||||||||
温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 |
频数 | 5 | 5 | 5 | 5 | 频数 | 6 | 4 | 4 | 6 | 频数 | 4 | 6 | 6 | 4 |
则在这20天中,甲、乙、丙三名同学的体温情况最稳定的是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com