
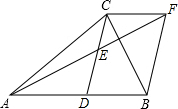
 如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.
如图.在△ABC中.CD是AB边的中线.E是CD中点,AE=EF.连结BF,CF.分析 (1)由SAS证明△AED≌△FEC,得出对应边相等AD=CF.再由DB=AD,即可得出结论.
(2)由全等三角形的性质得出∠ADE=∠FCE,证出DB∥CF,得出四边形BDCF是平行四边形,再由等腰三角形的三线合一性质得出CD⊥AB.即可得出结论;
(3)证明△ABC是等边三角形,DB=$\frac{1}{2}$AB=1,得出BC=2DB=2,由勾股定理求出CD,即可得出四边形的面积.
解答 (1)证明:∵CD是AB边的中线,E是CD中点,
∴AD=DB,DE=CE,
在△AED和△FEC中,$\left\{\begin{array}{l}{AE=EF}&{\;}\\{∠AED=∠FEC}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△AED≌△FEC(SAS).
∴AD=CF.
∵DB=AD,
∴DB=CF.
(2)解:由(1)得:△AED≌△FEC,
∴∠ADE=∠FCE,
∴DB∥CF,
∵DB=CF,
∴四边形BDCF是平行四边形,
∵AC=BC,D是AB的中点,
∴CD⊥AB.
∴∠CDB=90°,
∴四边形BDCF是矩形.
(3)解:∵∠ABC=60°,AB=2,AC=BC,
∴△ABC是等边三角形,DB=$\frac{1}{2}$AB=1,
∴BC=2DB=2,
∴CD=$\sqrt{B{C}^{2}-D{B}^{2}}$=$\sqrt{3}$,
∴四边形BDCF的面积=DB•CD=1×$\sqrt{3}$=$\sqrt{3}$.
点评 本题考查了全等三角形的判定与性质、矩形的判定与性质、等腰三角形的性质、等边三角形的判定与性质、勾股定理等知识;本题综合性强,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省襄阳老河口九年级3月月考数学试卷(解析版) 题型:单选题
下列计算正确的是( )
A. (3xy2) 2=6xy4 B. a+2a2=3a3 C. (-x) 7÷(-x) 2=-x5 D. 3x2+4x2=7x4
查看答案和解析>>
科目:初中数学 来源:2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷(解析版) 题型:填空题
某校甲乙两个体操队队员的平均身高相等,甲队队员身高的方差是S甲2=1.9,乙队队员身高的方差是S乙2=1.2,那么两队中队员身高更整齐的是__队.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
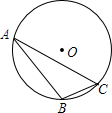 如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π.
如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则弦BC所对的弧长是$\frac{2}{5}$π或$\frac{8}{5}$π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com