练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知点P（a-1，a+5）在第二象限，且到y轴的距离为2，则点P的坐标为（-2，4）．

    分析 直接利用第二象限点的坐标性质结合到y轴的距离为2，得出a的值，进而得出点P的坐标．

    解答 解：∵点P（a-1，a+5）在第二象限，且到y轴的距离为2，
    ∴a-1=-2，
    解得：a=-1，
    ∴a+5=4，
    则点P的坐标为：（-2，4）．
    故答案为：（-2，4）．

    点评 此题主要考查了点的坐标，正确利用坐标性质得出a的值是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．逆用同底数幂相除的运算性质，能够解决一些从正面考虑较难解决的问题．
    例如，如果10x=5，求101-x的值．
    解：因为10x=5，所以101-x=10÷5=2．
    （逆用am÷an=am-n）
    那么当4x=9时，计算21-2x的值是多少？？

    查看答案和解析>>

    科目：初中数学 来源：2017届江苏省连云港市灌云县西片九年级下学期第一次月考数学试卷（解析版） 题型：判断题

    如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度AC=1.5m，CD=8m，则树高AB=__m．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

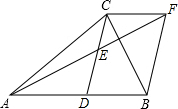    9．如图．在△ABC中．CD是AB边的中线．E是CD中点，AE=EF．连结BF，CF．
    （1）求证：DB=CF；
    （2）若AC=BC，求证：BDCF为矩形；
    （3）在（2）的情况下，若∠ABC=60°，AB=2，求BDCF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在升旗结束后，小铭想利用所学数学知识测量学校旗杆高度，如图，旗杆的顶端垂下一绳子，将绳子拉直钉在地上，末端恰好至C处且与地面成60°角，小铭从绳子末端C处拿起绳子后退至E点，求旗杆AB的高度和小铭后退的距离．（单位：米，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，结果保留一位小数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．先化简，再求值：（1-$\frac{1}{x-1}$）÷$\frac{1}{{x}^{2}-2x+1}+3x-4$，其中x=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．张村计划将自来水管道进行改装，该工程若由甲队单独施工恰好在规定时间内完成；若由乙队单独施工，则完成工程所需天数是规定天数的1.5倍，如果由甲、乙两队先合作15天，那么余下的工程由甲队单独完成还需5天．
    （1）这项工程的规定时间是多少天？
    （2）已知甲队每天的施工费用为6000元，乙队每天的施工费用为3000元．为了缩短工期，张村最终决定该工程由甲、乙队合作来完成．求该工程施工费用是多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．阅读材料：如果一个花坛的长，宽分别是m、n，且m、n满足m2-2mn+2n2-4n+4=0，求花坛的面积．
    解：∵m2-2mn+2n2-4n+4=0，∴（m2-2mn+n2）+（n2-4n+4）=0
    ∴（m-n）2+（n-2）2=0，∴（m-n）2=0，（n-2）2=0，∴m=n，n=2．
    ∴mn=4
    根据你的观察和思考，探究下面的问题：
    （1）若x2-2xy+5y2+4y+1=0，求xy的值；
    （2）若5x2+y2+z2+4xy-2xz=0，求代数式x-y-3z的值；
    （3）若△ABC的三边长a、b、c都是正整数，且满足a2+b2-10a-12b+61=0，求△ABC的周长的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：
    （1）16-（-10+3）+（-2）
    （2）（-4）2×$\frac{1}{8}$-27÷（-3）3．

    查看答案和解析>>

    同步练习册答案