
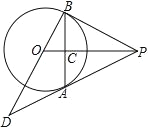
【题目】如图,PA 为⊙O 的切线,A 为切点,过 A 作弦 AB⊥OP,垂足为点 C,延长BO 与 PA 的延长线交于点 D
(1) 求证:PB 为⊙O 的切线
(2) 若 OB=3,OD=5,求 PB 的长
【答案】(1) 见详解;(2) PB=6.
【解析】
(1) 连接OA,根据垂径定理,得到PB=PA,可证明△PAO≌△PBO,因为PA 为⊙O 的切线,所以∠PBO=∠PAO=90°,题目得证;
(2)用勾股定理算出AD,由(1)中△PAO≌△PBO,得到PA=PB,设PB=x,△BDP为直角三角形,利用勾股定理列出等式,求解得出x,即为PB的长.
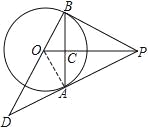
(1)证明:连接OA,
∵PA为⊙O的切线,
∴OA⊥PA
∴∠PAO=90°,
∵OA=OB,OP⊥AB于C,
∴PB=PA,
∴△PAO≌△PBO,
∴∠PBO=∠PAO=90°,
∴PB为⊙O的切线;
(2)在直角三角形OAD中,
![]() ,
,
BD=OB+OD=8,
∵△PAO≌△PBO,
∴PA=PB,
设PB=x,
∵PB 为⊙O 的切线,
∴∠DBP=90°,△BDP为直角三角形,
∴BD+BP=DP2,即8+x=(4+x),
解得x=6,
∴PB=6.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,BC为⊙O的直径,点E为△ABC的内心,连接AE并延长交⊙O于D点,连接BD并延长至F,使得BD=DF,连接CF、BE.
(1)求证:DB=DE;
(2)求证:直线CF为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
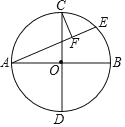
【题目】如图,在⊙O 中,AB、CD是互相垂直的两条直径,点E在![]() 上,CF⊥AE 于点F,若点F四等分弦AE,且AE=8,则⊙O 的面积为______.
上,CF⊥AE 于点F,若点F四等分弦AE,且AE=8,则⊙O 的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
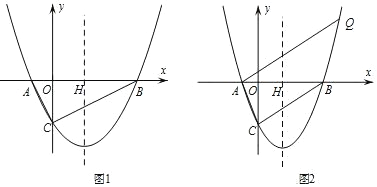
【题目】已知,抛物线 y=![]() x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=
x2+bx+c 与 y 轴交于点 C,与 x 轴交于点 A 和点B(其中点 A 在 y 轴左侧,点 B 在 y 轴右侧),对称轴直线 x=![]() 交 x 轴于点 H.
交 x 轴于点 H.
(1)若抛物线y=![]() x2+bx+c经过点(﹣4,6),求抛物线的解析式;
x2+bx+c经过点(﹣4,6),求抛物线的解析式;
(2)如图1,∠ACB=90°,点P是抛物线y=![]() x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
x2+bx+c上位于y轴右侧的动点,且 S△ABP=S△ABC,求点 P 的坐标;
(3)如图 2,过点A作AQ∥BC交抛物线于点Q,若点Q的纵坐标为﹣![]() c, 求点Q的坐标.
c, 求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
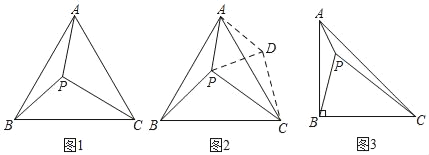
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C , 连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
A. 6 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.

(1)三角尺旋转了 度。
(2)连接CD,试判断△CBD的形状;
(3)求∠BDC的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
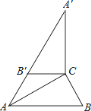
【题目】(1)如图1,点P是等边△ABC内一点,已知PA=3,PB=4,PC=5,求∠APB的度数.
要直接求∠A的度数显然很因难,注意到条件中的三边长恰好是一组勾股数,因此考虑借助旋转把这三边集中到一个三角形内,如图2,作∠PAD=60°使AD=AP,连接PD,CD,则△PAD是等边三角形.
∴ =AD=AP=3,∠ADP=∠PAD=60°
∵△ABC是等边三角形
∴AC=AB,∠BAC=60°
∴∠BAP=
∴△ABP≌△ACD
∴BP=CD=4, =∠ADC
∵在△PCD中,PD=3,PC=5,CD=4,PD2+CD2=PC2
∴∠PDC= °
∴∠APB=∠ADC=∠ADP+∠PDC=60°+90°=150°
(2)如图3,在△ABC中,AB=BC,∠ABC=90°,点P是△ABC内一点,PA=1,PB=2,PC=3,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
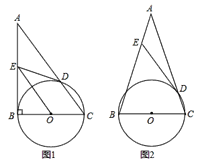
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com