
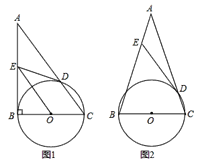
【题目】如图,以△ABC的边BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点E.
(1)如图1,若∠ABC=90°,求证:OE∥AC;
(2)如图2,已知AB=AC,若sin∠ADE=![]() , 求tanA的值.
, 求tanA的值.
【答案】(1)详见解析;(2)tan∠A=![]() .
.
【解析】
(1)连结OD,如图1,先根据切线的性质得到∠ODE=90°,然后通过HL证明Rt△OBE≌Rt△ODE,得到∠1=∠2,利用三角形的外角性质得到∠2=∠C,再根据平行线的判定定理即可得证;
(2)连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,易证∠A=∠COD,根据切线的性质与两角互余可得∠ADE=∠DOF,则在Rt△DOF中,sin∠DOF=![]() =
=![]() ,设DF=x,则OD=3x,然后用含x的式子表示相关线段的长,然后求得tanA的值即可.
,设DF=x,则OD=3x,然后用含x的式子表示相关线段的长,然后求得tanA的值即可.
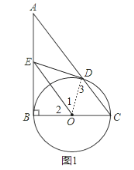
解:(1)证明:连结OD,如图1,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
在Rt△OBE和Rt△ODE中,
![]() ,
,
∴Rt△OBE≌Rt△ODE,
∴∠1=∠2,
∵OC=OD,
∴∠3=∠C,
而∠1+∠2=∠C+∠3,
∴∠2=∠C,
∴OE∥AC;
(2)解:连结OD,作OF⊥CD于F,DH⊥OC于H,如图2,
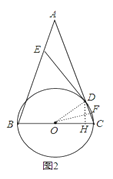
∵AB=AC,OC=OD,
而∠ACB=∠OCD,
∴∠A=∠COD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,
∴∠ADE+∠ODF=90°,
而∠DOF+∠ODF=90°,
∴∠ADE=∠DOF,
∴sin∠DOF=sin∠ADE=![]() ,
,
在Rt△DOF中,sin∠DOF=![]() =
=![]() ,
,
设DF=x,则OD=3x,
∴OF=![]() =2
=2![]() x,DF=CF=x,OC=3x,
x,DF=CF=x,OC=3x,
∵![]() DHOC=
DHOC=![]() OFCD,
OFCD,
∴DH=![]() =
=![]() x,
x,
在Rt△ODH中,OH=![]() =
=![]() x,
x,
∴tan∠DOH=![]() =
=![]() =
=,
∴tan∠A=![]() .
.


科目:初中数学 来源: 题型:
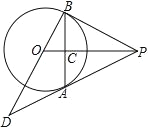
【题目】如图,PA 为⊙O 的切线,A 为切点,过 A 作弦 AB⊥OP,垂足为点 C,延长BO 与 PA 的延长线交于点 D
(1) 求证:PB 为⊙O 的切线
(2) 若 OB=3,OD=5,求 PB 的长
查看答案和解析>>
科目:初中数学 来源: 题型:
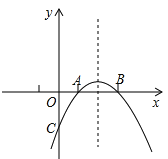
【题目】已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从热气球C处测得地面A,B两点的俯角分别为30°,45°,此时热气球C处所在位置到地面上点A的距离为400米.求地面上A,B两点间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
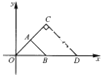
【题目】如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
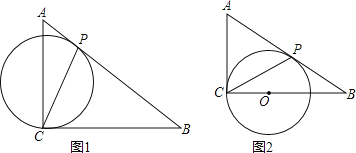
【题目】如图1,Rt△ACB中,AC=3,BC=4,有一动圆⊙O始终与Rt△ACB的斜边AB相切于动点P,且⊙O始终经过直角顶点C.
(1)如图2,当⊙O 运动至与直角边AC相切时,求此时⊙O 的半径r的长;
(2)试求⊙O 的半径r的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
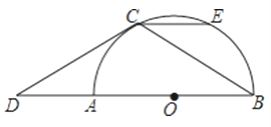
【题目】如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.
(1)求∠D的度数;
(2)求证:以点C,O,B,E为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解答:
题目:已知方程x2+3x+1=0的两根为a,b,求![]() 的值.
的值.
解:①∵△=b2﹣4ac=32﹣4×1×1=5>0∴a≠b
②由一元二次方程根与系数关系得:a+b=﹣3,ab=1;
③∴![]()
问题:上面的解题过程是否正确?若不正确,指出错在哪一步?写出正确的解题过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com