练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，从热气球C处测得地面A，B两点的俯角分别为30°，45°，此时热气球C处所在位置到地面上点A的距离为400米．求地面上A，B两点间的距离．

    【答案】AB=200+200（米）．

    【解析】

    试题分析：如图，过点C作CD⊥AB于点D，构建直角△ACD和直角△BCD，通过解这两个直角三角形求AD、BD的长度，则易求AB=AD+BD．

    试题解析：如图，过点C作CD⊥AB于点D，

    在直角△ACD中，∠A=30°，AC=400米，则AD=ACcos30°=400×=200（米），CD=AC=200米．

    在直角△BCD中，∠B=45°，∠CDB=90°，则∠BCD=∠B=45°，

    所以BD=CD=200米，

    所以AB=AD+BD=200+200（米）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知一次函数y＝﹣2x+4，完成下列问题：

    （1）在所给直角坐标系中画出此函数的图象；

    （2）根据函数图象回答：

    方程﹣2x+4＝0的解是______________；当x_____________时，y＞2；当﹣4≤y≤0时，相应x的取值范围是_______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若抛物线L：y=ax2+bx+c（a，b，c是常数，且abc≠0）与直线l都经过y轴上的同一点，且抛物线L的顶点在直线l上，则称此抛物线L与直线l具有“一带一路”关系，并且将直线l叫做抛物线L的“路线”，抛物线L叫做直线l的“带线”．

    （1）若“路线”l的表达式为y=﹣x+2，它的“带线”L的顶点在反比例函数y=的图象上，求“带线”L的表达式；

    （2）如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系，求m，n的值；

    （3）设（2）中的“带线”L与它的“路线”l在y轴上的交点为A．已知点P为“带线”L上的点，当以点P为圆心的圆与“路线”l相切于点A时，求出点P的坐标

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了开展读书月活动，对学生最喜欢的图书种类进行了一次抽样调查，所有图书分成四类：艺术、文学、科普、其他．随机调查了该校m名学生（每名学生必选且只能选择一类图书），并将调查结果制成如下两幅不完整的统计图：

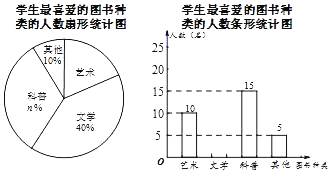
    根据统计图提供的信息，解答下列问题：

    （1）m＝　 　，n＝　 　，并请根据以上信息补全条形统计图；

    （2）扇形统计图中，“艺术”所对应的扇形的圆心角度数是　 　度；

    （3）根据抽样调查的结果，请你估计该校900名学生中有多少学生最喜欢科普类图书．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数y=的图象经过点A（x1，y1）和B（x2，y2）（x1＜x2）

    （1）若A（4，n）和B（n+，3），求反比例函数的表达式；

    （2）若m=1，

    ①当x2=1时，直接写出y1的取值范围；

    ②当x1＜x2＜0，p=，q=，试判断p，q的大小关系，并说明理由；

    （3）若过A、B两点的直线y=x+2与y轴交于点C，连接BO，记△COB的面积为S，当＜S＜1，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD中，BD⊥AD，∠A=45°，E、F分别是AB，CD上的点，且BE=DF，连接EF交BD于O．

    （1）求证：BO=DO；

    （2）若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

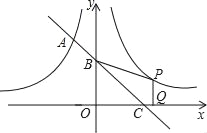
    【题目】如图，一次函数的图象与反比例函数的图象相交于A点，与y轴、x轴分别相交于B、C两点，且C（2，0）．当x＜﹣1时，一次函数值大于反比例函数值，当x＞﹣1时，一次函数值小于反比例函数值．

    (1)求一次函数的解析式；

    (2)设函数y2=的图象与的图象关于y轴对称，在y2=的图象上取一点P（P点的横坐标大于2），过P作PQ丄x轴，垂足是Q，若四边形BCQP的面积等于2，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

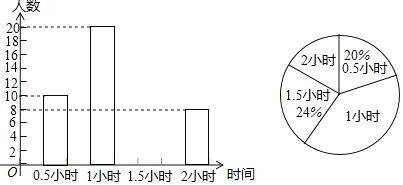
    【题目】为增强学生的身体素质，教育行政部门规定学生每天参加户外活动的平均时间不少于1小时．为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制作成如下两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

    （1）补全频数分布直方图；

    （2）表示户外活动时间1小时的扇形圆心角的度数是多少；

    （3）本次调查学生参加户外活动时间的众数是多少，中位数是多少；

    （4）本次调查学生参加户外活动的平均时间是否符合要求？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，四边形ABCD中，AD∥BC，AD=CD，E是对角线BD上一点，且EA=EC．

    （1）求证：四边形ABCD是菱形；

    （2）如果BE=BC，且∠CBE：∠BCE=2：3，求证：四边形ABCD是正方形．

    查看答案和解析>>

    同步练习册答案