
����Ŀ����������L��y=ax2+bx+c��a��b��c�dz�������abc��0����ֱ��l������y���ϵ�ͬһ�㣬��������L�Ķ�����ֱ��l�ϣ���ƴ�������L��ֱ��l���С�һ��һ·����ϵ�����ҽ�ֱ��l����������L�ġ�·�ߡ���������L����ֱ��l�ġ����ߡ���
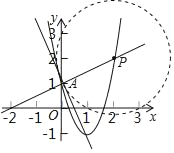
��1������·�ߡ�l�ı���ʽΪy=��x+2�����ġ����ߡ�L�Ķ����ڷ���������y=![]() ��ͼ���ϣ����ߡ�L�ı���ʽ��
��ͼ���ϣ����ߡ�L�ı���ʽ��
��2�����������y=mx2��2mx+m��1��ֱ��y=nx+1���С�һ��һ·����ϵ����m��n��ֵ��
��3���裨2���еġ����ߡ�L�����ġ�·�ߡ�l��y���ϵĽ���ΪA����֪��PΪ�����ߡ�L�ϵĵ㣬���Ե�PΪԲ�ĵ�Բ�롰·�ߡ�l�����ڵ�Aʱ�������P������
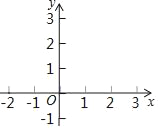
���𰸡���1�� �����ߡ�L�Ľ���ʽΪy=x2��2x+2����2��m��n��ֵ�ֱ�Ϊ2����2����3��P������Ϊ��![]() ��
��![]() ����
����
��������
��1�������¶��壬ͨ���ⷽ����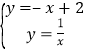 �ô��ߡ�L�Ķ�������Ϊ��1��1�����������·�ߡ�l��y��Ľ�������Ϊ��0��2�����������⡱���ߡ�L�����㣨0��2����Ȼ�����ô���ϵ��������ߡ�L�Ľ���ʽ��
�ô��ߡ�L�Ķ�������Ϊ��1��1�����������·�ߡ�l��y��Ľ�������Ϊ��0��2�����������⡱���ߡ�L�����㣨0��2����Ȼ�����ô���ϵ��������ߡ�L�Ľ���ʽ��
��2����ȷ��ֱ��y=nx+1��y��Ľ�������Ϊ��0��1���������¶���ѣ�0��1������y=mx2��2mx+m��1�ɵ�m=2�������ö��κ��������ʵõ������ߵĶ�������Ϊ��1����1����
Ȼ��Ѷ����������y=nx+1�пɵõ�n��ֵ��
��3���ɣ�2����A��0��1������PA��ֱ��y=��2x+1����������P����ͼ��������һ�κ�����ֱһ����ϵ���Ĺ�ϵ�õ�ֱ��PA�Ľ���ʽΪy=![]() x+1��Ȼ��ͨ���ⷽ����
x+1��Ȼ��ͨ���ⷽ���� 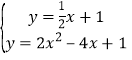 ��P�����꣮
��P�����꣮
��1���ⷽ����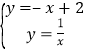 ��
��![]() ������ߡ�L�Ķ�������Ϊ��1��1����
������ߡ�L�Ķ�������Ϊ��1��1����
��x=0ʱ��y=��x+2=2����·�ߡ�l��y��Ľ�������Ϊ��0��2����
�������⡱���ߡ�L�����㣨0��2����
�衰���ߡ�L�Ľ���ʽΪy=a��x��1��2+1��
�ѣ�0��2�������a+1=2�����a=1��
�ࡰ���ߡ�L�Ľ���ʽΪy=��x��1��2+1����y=x2��2x+2��
��2����x=0ʱ��y=nx+1=1����ֱ��y=nx+1��y��Ľ�������Ϊ��0��1����
�ѣ�0��1������y=mx2��2mx+m��1��m��1=1�����m=2��
�������߽���ʽΪy=2x2��4x+1��
��y=��x��1��2��1��
�������ߵĶ�������Ϊ��1����1����
�ѣ�1����1������y=nx+1��n+1=��1�����n=��2��
��m��n��ֵ�ֱ�Ϊ2����2��
��3���ɣ�2����A��0��1����
��PA��ֱ��y=��2x+1����������P����ͼ��
��ֱ��PA�Ľ���ʽΪy=![]() x+t��
x+t��
��A��0��1�������t=1��
��ֱ��PA�Ľ���ʽΪy=![]() x+1��
x+1��
�ⷽ����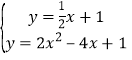 ��
��![]() ��
��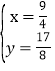 ��
��
��P��������![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̲ij��֣���ͼ�ǻ�ʦ����꼶�ϲ���ѧ�̲ĵ�96ҳ�IJ������ݣ�
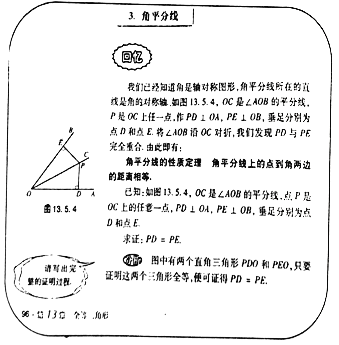

����ݽ̲��еķ��������ͼ�٣�д������ƽ���ߵ����ʶ�����������֤�����̣�
����Ӧ�ã�
��ͼ�ڣ����ı���ABCD�У���B����C����E�ڱ�BC�ϣ�AEƽ�֡�BAD��DEƽ�֡�ADC��
��1����֤��BE��CE��
��2�����ı���ABCD���ܳ�Ϊ24��BE��2�����Ϊ30�����ABE�ı�AB�ĸߵij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��ѧ�������й���У�����������ִ������ߡ����в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��

��1������ͼʾ��д�±���
ƽ�������֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |
��2��������ӳɼ���ƽ��������λ���������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ���ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
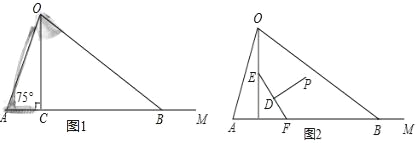
����Ŀ����ͼ1Ϊ������ˮƽ�����ϵ�̨�Ƶ�ƽ��ʾ��ͼ���Ʊ�AO��Ϊ50cm����ˮƽ�������γɵļн���OAM Ϊ75�㣮�ɹ�ԴO����ı�Ե����OC��OB ��ˮƽ�������γɵļн���OCA����OBA�ֱ�Ϊ90���30�㣮���������������أ������ȷ��0.1cm��sin75����0.97��cos75���0.26��![]() ��1.73��
��1.73��
��1�����̨������ˮƽ����Ŀ���BC��
��2�������ڴ�̨���¿��飬�������������ͼ2��ʾ�ļ���ͼ�Σ�����EF��ˮƽ����ļн���EFCΪ60�㣬��ij���EFΪ24cm����PΪ�۾�����λ�ã���P��EF�Ĵ�ֱƽ�����ϣ��ҵ�EF����ԼΪ34cm�����۾���ˮƽ����ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
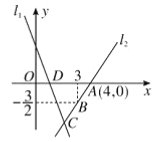
����Ŀ����ͼ��ֱ��![]() �Ľ�������ʽΪ
�Ľ�������ʽΪ![]() ����
����![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() .ֱ��
.ֱ��![]() ������
������![]() ��ֱ��
��ֱ��![]() ���ڵ�
���ڵ�![]() ��
��
��1�����![]() �����ꣻ
�����ꣻ
��2����ֱ��![]() �Ľ�������ʽ��
�Ľ�������ʽ��
��3����![]() ��������һ��
��������һ��![]() ��ʹ
��ʹ![]() �ĺ���С��ֱ��д��
�ĺ���С��ֱ��д��![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������߳�Ϊ![]() ��������ABCD�У�C��0��5������A��x���ϣ���B�ڷ���������y=
��������ABCD�У�C��0��5������A��x���ϣ���B�ڷ���������y=![]() ��x��0��m��0����ͼ���ϣ���D�ڷ���������y=
��x��0��m��0����ͼ���ϣ���D�ڷ���������y=![]() ��x��0��n��0����ͼ���ϣ���ôm+n=______��
��x��0��n��0����ͼ���ϣ���ôm+n=______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������C����õ���A��B����ĸ��Ƿֱ�Ϊ30�㣬45�㣬��ʱ������C������λ�õ������ϵ�A�ľ���Ϊ400�ף��������A��B�����ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
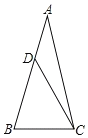
����Ŀ����ͼ����ABC�У�AB=AC����A=30�㣬��D�ڱ�AB�ϣ���ACD=15�㣬��![]() ____��
____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com