
����Ŀ����ͼ1Ϊ������ˮƽ�����ϵ�̨�Ƶ�ƽ��ʾ��ͼ���Ʊ�AO��Ϊ50cm����ˮƽ�������γɵļн���OAM Ϊ75�㣮�ɹ�ԴO����ı�Ե����OC��OB ��ˮƽ�������γɵļн���OCA����OBA�ֱ�Ϊ90���30�㣮���������������أ������ȷ��0.1cm��sin75����0.97��cos75���0.26��![]() ��1.73��
��1.73��
��1�����̨������ˮƽ����Ŀ���BC��
��2�������ڴ�̨���¿��飬�������������ͼ2��ʾ�ļ���ͼ�Σ�����EF��ˮƽ����ļн���EFCΪ60�㣬��ij���EFΪ24cm����PΪ�۾�����λ�ã���P��EF�Ĵ�ֱƽ�����ϣ��ҵ�EF����ԼΪ34cm�����۾���ˮƽ����ľ��룮
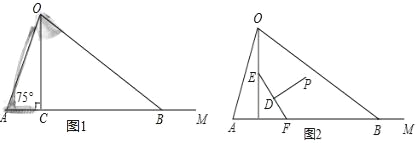
���𰸡���1����̨������ˮƽ��Ŀ���BC��Լ��83.9cm����2���۾���ˮƽ����ľ����Լ��27.38cm��
��������
��1����ֱ��������ACO�У�����sin75��=![]() �����OC����ֱ��������BCO�У�tan30��=
�����OC����ֱ��������BCO�У�tan30��=![]() �����BC���ɣ�
�����BC���ɣ�
��2����ͼ������P��PH��AB��H����OB��M������D��DG��PH��G��DQ��AB��Q�����ı���DGHQΪ���Σ���GDF=��EFC=��DPG=60�㣬���PH�ij�������⣮
��1����ֱ��������ACO�У�sin75��= ![]() ��
��
���OC=50��0.97��48.5��
��ֱ��������BCO�У�tan30��=![]() ��
��
���BC=1.73��48.5��83.9��
�𣺸�̨������ˮƽ��Ŀ���BC��Լ��83.9cm��
��2����ͼ2������P��PH��AB��H������D��DG��PH��G��DQ��AB��Q��
���ı���DGHQΪ���Σ���GDF=��EFC=��DPG=60��
������DE=DF=12cm��DP=34cm��
��PG=17cm��QH=DG=17![]() cm��QF=6cm��GH=DQ=6
cm��QF=6cm��GH=DQ=6![]() cm��
cm��
��PH=PH+GH=17+6![]() ��27.38cm��
��27.38cm��
���۾���ˮƽ����ľ����Լ��27.38cm��


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��࣬���ȱ�������ADE��AC��BE�ཻ�ڵ�F�����BFCΪ��������

A. 75��B. 60��C. 55��D. 45��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
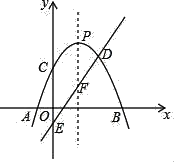
����Ŀ����ͼ��������L��y=����x��2��2+m2+2m��x�ύ��A��B��ֱ��y=kx��1��y�ύ��E����L�ĶԳ��ύ�ڵ�F��n��3������L����D��������L�ĶԳ�����L����P��
(1)��k��ֵ��
(2)��P�ܷ����F����x��ĶԳƵ��غϣ�����Ϊ�ܣ������m��ֵ������Ϊ���ܣ�˵�����ɣ�
(3)С���о���������L�Ľ���ʽ�õ������µĽ��ۣ���Ϊm����ȡ����ʵ�������Ե�C������y���������ƶ�����C����Ե���y����κ�λ�ã�����Ϊ��˵���е�����˵˵����뷨��
(4)��������L��ֱ��y=kx��1������������ʱ��ֱ��д���ʺ�������m�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˷ֱ��A��B����ͬʱ������������У�����ǰ��B�ء�A�أ���������ʱͣ����4min���ָ���ԭ��ǰ��Ŀ�ĵأ��ס�������֮��ľ���y��m���������ʱ��x��min��֮��ĺ�����ϵ��ͼ��ʾ��������˵����

��A��B֮��ľ���Ϊ1200m�� �������ߵ��ٶ��Ǽ�1.5������ b=960�� �� a=34��
���Ͻ�����ȷ���У�������
A. �٢� B. �٢ڢ� C. �٢ۢ� D. �٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����2014��Ͷ���������2900��Ԫ��2016��Ͷ���������3509��Ԫ��
��1����2014����2016��õ���Ͷ��������ѵ���ƽ�������ʣ�
��2����������������涨���������ѵ�Ͷ�벻���ڹ���������ֵ�İٷ�֮�ģ���ϸõ�������������ֵ������������õ�����2018����Ͷ���������4250��Ԫ���������1���н�������Ͷ��������ʣ���2018��õ���Ͷ��Ľ��������Ƿ��ܴﵽ4250��Ԫ����˵�����ɣ�
���ο����ݣ� ![]() =1.1��
=1.1�� ![]() =1.2��
=1.2�� ![]() =1.3��
=1.3�� ![]() =1.4��
=1.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������L��y=ax2+bx+c��a��b��c�dz�������abc��0����ֱ��l������y���ϵ�ͬһ�㣬��������L�Ķ�����ֱ��l�ϣ���ƴ�������L��ֱ��l���С�һ��һ·����ϵ�����ҽ�ֱ��l����������L�ġ�·�ߡ���������L����ֱ��l�ġ����ߡ���
��1������·�ߡ�l�ı���ʽΪy=��x+2�����ġ����ߡ�L�Ķ����ڷ���������y=![]() ��ͼ���ϣ����ߡ�L�ı���ʽ��
��ͼ���ϣ����ߡ�L�ı���ʽ��
��2�����������y=mx2��2mx+m��1��ֱ��y=nx+1���С�һ��һ·����ϵ����m��n��ֵ��
��3���裨2���еġ����ߡ�L�����ġ�·�ߡ�l��y���ϵĽ���ΪA����֪��PΪ�����ߡ�L�ϵĵ㣬���Ե�PΪԲ�ĵ�Բ�롰·�ߡ�l�����ڵ�Aʱ�������P������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��600�����μ���Ʒ������Ϊÿ��6Ԫ����һ����ÿ��10Ԫ�ļ۸��۳�200�����ڶ�������ÿ��10Ԫ�ļ۸������Կ��۳�200�������̵�Ϊ���ʵ����������������������ۣ������г����飬����ÿ����1Ԫ���ɶ��۳�50�������ۼ۲��õ��ڽ��ۣ������۽���xԪ��������һ�ܺ��̵��ʣ�����μ���Ʒ��ִ�������ÿ��4Ԫ�ļ۸�ȫ���۳�������������μ���Ʒ������1250Ԫ���ʵڶ���ÿ�����μ���Ʒ�����ۼ۸�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=![]() ��ͼ����A��x1��y1����B��x2��y2����x1��x2��
��ͼ����A��x1��y1����B��x2��y2����x1��x2��
��1����A��4��n����B��n+![]() ��3�������������ı���ʽ��
��3�������������ı���ʽ��
��2����m=1��
�ٵ�x2=1ʱ��ֱ��д��y1��ȡֵ��Χ��
�ڵ�x1��x2��0��p=![]() ��q=
��q=![]() �����ж�p��q�Ĵ�С��ϵ����˵�����ɣ�
�����ж�p��q�Ĵ�С��ϵ����˵�����ɣ�
��3������A��B�����ֱ��y=x+2��y�ύ�ڵ�C������BO���ǡ�COB�����ΪS����![]() ��S��1����m��ȡֵ��Χ��
��S��1����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ۿ�Pλ�ڶ�������ĺ������ϣ���Զ�����š������족���ִ�ͬʱ�뿪�ۿڣ�������һ�̶������У���Զ������ÿСʱ����16��������족��ÿСʱ����12��������뿪�ۿ�һ����Сʱ��ֱ�λ�ڵ�Q��R���������30������֪����Զ�������ض��������У����족����(����)�����У�

A.����B.����C.����D.����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com