
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
【答案】(1)证明见解析,(2)2![]() .
.
【解析】
试题分析:(1)通过证明△ODF与△OBE全等即可求得.
(2)由△ADB是等腰直角三角形,得出∠A=45°,因为EF⊥AB,得出∠G=45°,所以△ODG与△DFG都是等腰直角三角形,从而求得DG的长和EF=2,然后等腰直角三角形的性质即可求得.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴DC=AB,DC∥AB,
∴∠ODF=∠OBE,
在△ODF与△OBE中
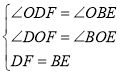
∴△ODF≌△OBE(AAS)
∴BO=DO;
(2)解:∵BD⊥AD,
∴∠ADB=90°,
∵∠A=45°,
∴∠DBA=∠A=45°,
∵EF⊥AB,
∴∠G=∠A=45°,
∴△ODG是等腰直角三角形,
∵AB∥CD,EF⊥AB,
∴DF⊥OG,
∴OF=FG,△DFG是等腰直角三角形,
∵△ODF≌△OBE(AAS)
∴OE=OF,
∴GF=OF=OE,
即2FG=EF,
∵△DFG是等腰直角三角形,
∴DF=FG=1,∴DG=![]() =DO,
=DO,
∴在等腰RT△ADB 中,DB=2DO=2![]() =AD
=AD
∴AD=2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在一次主题为“学会生存”的中学生社会实践活动中,春华同学为了锻炼自己,他通过了解市场行情,以每件![]() 元的价格从批发市场购进若干件印有
元的价格从批发市场购进若干件印有![]() 北京奥运标志的文化衫到自由市场去推销,当销售完
北京奥运标志的文化衫到自由市场去推销,当销售完![]() 件之后,销售金额达到
件之后,销售金额达到![]() 元,余下的每件降价
元,余下的每件降价![]() 元,很快推销完毕,此时销售金额达到
元,很快推销完毕,此时销售金额达到![]() 元,春华同学在这次活动中获得纯收入_______元.
元,春华同学在这次活动中获得纯收入_______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时: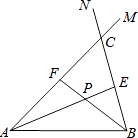
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ![]() ,求AQ的长.
,求AQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)这8筐白菜中最接近标准重量的这筐白菜重 ______ 千克;
(2)这8筐白菜中,最重的与最轻的相差______ 千克;
(3)这8筐白菜一共重多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E,F是对角线AC上的两点,且AE=CF.下列结论:①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE.其中正确的个数是( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月的某天小欣在“A超市”买了“雀巢巧克力”和“趣多多小饼干”共10包,已知“雀巢巧克力”每包22元,“趣多多小饼干”每包2元,总共花费了80元.
(1)请求出小欣在这次采购中,“雀巢巧克力”和“趣多多小饼干”各买了多少包?
(2)“五一”期间,小欣发现,A、B两超市以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在A超市累计购物超过50元后,超过50元的部分打九折;在B超市累计购物超过100元后,超过100元的部分打八折.
①请问“五一”期间,若小欣购物金额超过100元,去哪家超市购物更划算?
②“五一”期间,小欣又到“B超市”购买了一些“雀巢巧克力”,请问她至少购买多少包时,平均每包价格不超过20元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个圆柱体的侧面展开图为长方形ABCD,若AB=6.28cm,BC=18.84cm,则该圆柱体的体积是多少?(π取3.14,结果精确到十分位).

查看答案和解析>>
科目:初中数学 来源: 题型:
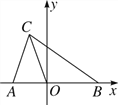
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且![]() +(4a-b+11)2=0.
+(4a-b+11)2=0.
(1)求a,b的值;
(2)在y轴的负半轴上存在一点M,使△COM的面积等于△ABC面积的一半,求出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com