
【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)这8筐白菜中最接近标准重量的这筐白菜重 ______ 千克;
(2)这8筐白菜中,最重的与最轻的相差______ 千克;
(3)这8筐白菜一共重多少千克?
【答案】(1) 这8筐白菜中最接近标准重量的这筐白菜重24.5千克;(2) 这8筐白菜中,最重的与最轻的相差5千克;(3) 这8筐白菜共重194.5千克
【解析】
根据正负数的意义,离原点最近的数表示最接近标准重量,越向右表示越重,越向左表示越轻;把各数相加可得比总标准重量多多少.
(1)25﹣0.5=24.5(千克).
答:这8筐白菜中最接近标准重量的这筐白菜重24.5千克;
(2)2﹣(﹣3)=5(千克).
答:这8筐白菜中,最重的与最轻的相差5千克;
(3)25×8+1.5﹣3+2﹣0.5+1﹣2﹣2.5﹣2
=200+4.5﹣10
=194.5(千克).
答:这8筐白菜共重194.5千克.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图1,已知数轴上两点A、B对应的数分别为﹣2、5,点P为数轴上的一动点,其对应的数为x.
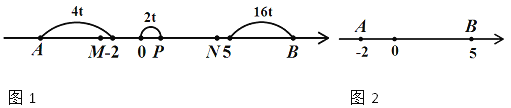
(1)PA= ;PB= (用含x的式子表示)
(2)在数轴上是否存在点P,使PA+PB=10?若存在,请直接写出x的值;若不存在,请说明理由.
(3)如图2,点P以2个单位/s的速度从点O向右运动,同时点A以4个单位/s的速度向左运动,点B以16个单位/s的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问: ![]() 的值是否发生变化?请说明理由.
的值是否发生变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 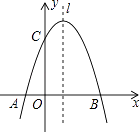
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab ![]()
D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
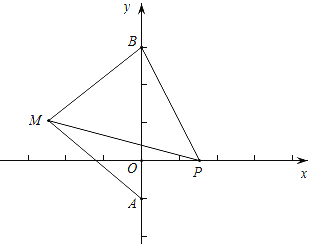
【题目】如图,在平面直角坐标系中,已知A(0,﹣1),B(0,3),点M为第二象限内一点,且点M的坐标为(t,1).
(1)请用含t的式子表示△ABM的面积;
(2)当t=﹣2时,在x轴的正半轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
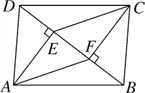
【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为点E,F.
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,再解答问题:
-5![]() +7
+7![]() =-5+(-
=-5+(-![]() )+7+
)+7+![]() =[(-5)+7]+[(-
=[(-5)+7]+[(-![]() )+
)+![]() ]=2+
]=2+![]() =2
=2![]() .
.
上述方法叫做拆项法,依照上述方法计算:
(1)7![]() +(-7
+(-7![]() );
);
(2)(-2018![]() )+(-2017
)+(-2017![]() )+4036
)+4036![]() +(-1
+(-1![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
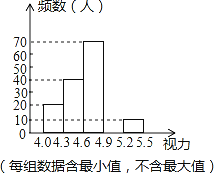
【题目】某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com