
【题目】在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
①∠APB=120°;②AF+BE=AB.
那么,当AM∥BN时: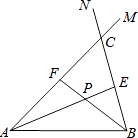
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出∠APB的度数,写出AF,BE,AB长度之间的等量关系,并给予证明;
(2)设点Q为线段AE上一点,QB=5,若AF+BE=16,四边形ABEF的面积为32 ![]() ,求AQ的长.
,求AQ的长.
【答案】
(1)
解:解:点点的结论:①∵∠ACB=60°,
∴∠BAC+∠ABC=120°,
∵∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,
∴∠PAB+∠PBA= ![]() (∠PAB+∠PBA)=60°,
(∠PAB+∠PBA)=60°,
∴∠APB=120°,
②如图,在AB上取一点G,使AG=AF,
∵AE是∠BAM的角平分线,
∴∠PAG=∠PAF,
在△PAG和△PAF中, 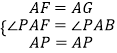 ,
,
∴△PAG≌△PAF(SAS),
∴∠AFP=∠AGP,
∵∠EPF=∠APB=120°,∠ACB=60°,
∴∠EPF+∠ACB=180°,
∴∠PFC+∠PEC=180°,
∵∠PFC+∠AFP=180°,
∴∠PEC=∠AFP,
∴∠PEC=∠AGP,
∵∠AGP+∠BGP=180°,
∴∠PEC+∠BGP=180°,
∵∠PEC+∠PEB=180°,
∴∠BGP=∠BEP,
∵BF是∠ABC的角平分线,
∴∠PBG=∠PBE,
在△BPG和△BPE中, 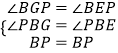 ,
,
∴△BPG≌△BPE(AAS),
∴BG=BE,
∴AF+BE=AB.
原命题不成立,新结论为:∠APB=90°,AF+BE=2AB(或AF=BE=AB),
理由:∵AM∥BN,
∴∠MAB+∠NBA=180°,
∵AE,BF分别平分∠MAB,NBA,
∴∠EAB= ![]() ∠MAB,∠FBA=
∠MAB,∠FBA= ![]() ∠NBA,
∠NBA,
∴∠EAB+∠FBA= ![]() (∠MAB+∠NBA)=90°,
(∠MAB+∠NBA)=90°,
∴∠APB=90°,
∵AE平分∠MAB,
∴∠MAE=∠BAE,
∵AM∥BN,
∴∠MAE=∠BAE,
∴∠BAE=∠BEA,
∴AB=BE,
同理:AF=AB,
∴AF+BE=2AB(或AF=BE=AB)
(2)
解:如图1,
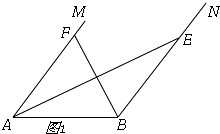
过点F作FG⊥AB于G,
∵AF=BE,AF∥BE,
∴四边形ABEF是平行四边形,
∵AF+BE=16,
∴AB=AF=BE=8,
∵32 ![]() =8×FG,
=8×FG,
∴FG=4 ![]() ,
,
在Rt△FAG中,AF=8,
∴∠FAG=60°,
当点G在线段AB上时,∠FAB=60°,
当点G在线段BA延长线时,∠FAB=120°,
①如图2,
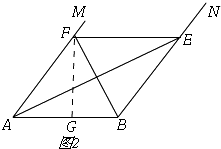
当∠FAB=60°时,∠PAB=30°,
∴PB=4,PA=4 ![]() ,
,
∵BQ=5,∠BPA=90°,
∴PQ=3,
∴AQ=4 ![]() ﹣3或AQ=4
﹣3或AQ=4 ![]() +3.
+3.
②如图3,
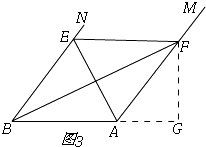
当∠FAB=120°时,∠PAB=60°,∠FBG=30°,
∴PB=4 ![]() ,
,
∵PB=4 ![]() >5,
>5,
∴线段AE上不存在符合条件的点Q,
∴当∠FAB=60°时,AQ=4 ![]() ﹣3或4
﹣3或4 ![]() +3.
+3.
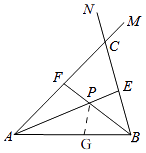
【解析】点点的两个结论:①利用三角形的角平分线和三角形的内角和即可得出结论;②先判断出△PAG≌△PAF(SAS)得出∠AFP=∠AGP,结合同角的补角相等即可得出∠BGP=∠BEP,进而判断出△BPG≌△BPE(AAS),即可得出结论;(1)由角平分线和平行线整体求出∠MAB+∠NBA,从而得到∠APB=90°,最后用等边对等角,即可.(2)先根据条件求出AF,FG,求出∠FAG=60°,最后分两种情况讨论计算.


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.
(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学生小刘回乡创办小微企业,初期购得原材料若干吨,每天生产相同件数的某种产品,单件产品所耗费的原材料相同.当生产6天后剩余原材料36吨,当生产10天后剩余原材料30吨.若剩余原材料数量小于或等于3吨,则需补充原材料以保证正常生产.
(1)求初期购得的原材料吨数与每天所耗费的原材料吨数;
(2)若生产16天后,根据市场需求每天产量提高20%,则最多再生产多少天后必须补充原材料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) 
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{ A,B }的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{ A,B }的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B }的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{ M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,到达点A停止.P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对下列代数式作出解释,其中不正确的是( )
A. a-b:今年小明b岁,小明的爸爸a岁,小明比他爸爸小(a-b)岁
B. a-b:今年小明b岁,小明的爸爸a岁,则小明出生时,他爸爸为(a-b)岁
C. ab:长方形的长为acm,宽为bcm,长方形的面积为ab ![]()
D. ab:三角形的一边长为acm,这边上的高为bcm,此三角形的面积为ab ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=10cm,AM=3cm,求CN的长;
(2)如果MN=6cm,求AB的长.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com