
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)首先证得△ADE≌△CDE,由全等三角形的性质可得∠ADE=∠CDE,由AD∥BC可得∠ADE=∠CBD,易得∠CDB=∠CBD,可得BC=CD,易得AD=BC,利用平行线的判定定理可得四边形ABCD为平行四边形,由AD=CD可得四边形ABCD是菱形;
(2)由BE=BC可得△BEC为等腰三角形,可得∠BCE=∠BEC,利用三角形的内角和定理可得∠CBE=180×![]() =45°,易得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形.
=45°,易得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形.
试题解析:(1)在△ADE与△CDE中,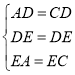 ,∴△ADE≌△CDE,∴∠ADE=∠CDE,
,∴△ADE≌△CDE,∴∠ADE=∠CDE,
∵AD∥BC,∴∠ADE=∠CBD,∴∠CDE=∠CBD,∴BC=CD,
∵AD=CD,∴BC=AD,∴四边形ABCD为平行四边形,
∵AD=CD,∴四边形ABCD是菱形;
(2)∵BE=BC,∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,∴∠CBE=180×![]() =45°,
=45°,
∵四边形ABCD是菱形,∴∠ABE=45°,∴∠ABC=90°,∴四边形ABCD是正方形.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省( ) 
A.1元
B.2元
C.3元
D.4元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,E是⊙O外一点,过点E作⊙O的两条切线ED、EB,切点分别为点D,B,连接AD并延长交BE延长线于点C,连接OE. 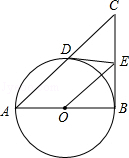
(1)试判断OE与AC的关系,并说明理由;
(2)填空: ①当∠BAC=时,四边形ODEB是正方形.
②当∠BAC=30°时, ![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)、B(3,0)两点,与y轴交于点C(0,3).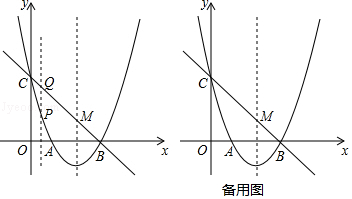
(1)求抛物线的解析式;
(2)设点P是位于直线BC下方的抛物线上一动点,过点P作y轴的平行线交直线BC于点Q,求线段PQ的最大值;
(3)在(2)的条件下,抛物线的对称轴与直线BC交于点M,问是否存在点P,使以M、P、Q为顶点的三角形与△CBO相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为56,则n=_.
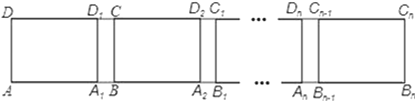
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.

(1)若∠ECD=60°,求∠AFC的度数;
(2)若∠ECD=∠BAF,试判断∠ABD与∠BDC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为实施“农村留守儿童关爱计划”,某校对全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成了如下两幅不完整的统计图: 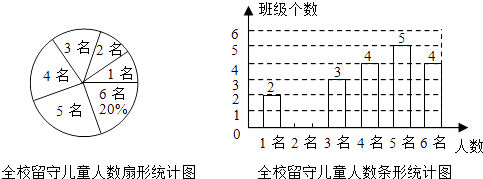
(1)将该条形统计图补充完整;
(2)求该校平均每班有多少名留守儿童?
(3)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,L1L2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数关系,则以下判断错误的是( )

A. 骑车的同学比步行的同学晚出发30分钟
B. 骑车的同学和步行的同学同时到达目的地
C. 骑车的同学从出发到追上步行的同学用了20分钟
D. 步行的速度是6千米/小时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com