Question

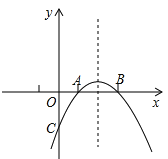
【题目】已知：如图所示，抛物线y=-x2+bx+c与x轴的两个交点分别为A（1，0），B（3，0）．

（1）求抛物线的解析式；

（2）设点P在该抛物线上滑动，且满足条件S△PAB=1的点P有几个？并求出所有点P的坐标；

（3）设抛物线交y轴于点C，问该抛物线对称轴上是否存在点M，使得△MAC的周长最小？若存在，求出点M的坐标；若不存在，请说明理由．

Answer 1

【答案】【答案（1）抛物线解析式为 ；

（2）满足条件的点P有三个坐标分别为（2，1），（，﹣1），（，﹣1）；

（3）存在点M（2，﹣1），可使△AMC的周长最小．

【解析】

（1）将A（1，0），B（3，0）代入抛物线中，列方程组可求抛物线解析式；

（2）由于AB=3﹣1=2，而，故△PAB中，AB边上的高为1，即P点纵坐标为±1，代入抛物线解析式可求P点横坐标；

（3）过点C作抛物线的对称轴的对称点C'，根据抛物线的对称性求得C′（4，﹣3），连接直线AC′，求直线AC′的解析式，直线AC′与对称轴的交点即为所求点M

解：（1）依题意有 ，

∴b=4，c=﹣3，

∴抛物线解析式为 ；

（2）如图，设P（x，y）

∵AB=2，

∴×2×|y|=1

∴y=±1

当y=1时，解得 ，

当y=﹣1时，解得，

∴满足条件的点P有三个坐标分别为（2，1），（，﹣1），（，﹣1）；

（3）存在．

过点C作抛物线的对称轴的对称点C'，如图

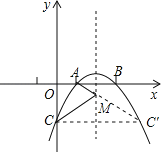
∵点C（0，﹣3），对称轴为x=2，

∴C′（4，﹣3），

设直线AC′的解析式为y=kx+b，

则，

∴k=﹣1，b=1，

∴直线AC′的解析式为y=﹣x+1，

直线AC′与对称轴x=2的交点为（2，﹣1），即M（2，﹣1），

∴存在点M（2，﹣1），可使△AMC的周长最小．