
【题目】已知二次函数y=ax2+bx+c的图象如图所示,下列结论:①9a﹣3b+c=0;②4a﹣2b+c>0;③方程ax2+bx+c﹣4=0有两个相等的实数根;④方程a(x﹣1)2+b(x﹣1)+c=0的两根是x1=﹣2,x2=2.其中正确结论的个数是_________.

【答案】4
【解析】
①根据x=-3时,对应的y=0,代入可得结论;
②根据x=-2时,对应的y>0,代入可得结论;
③根据顶点坐标中y=4,可得方程ax2+bx+c-4=0有两个相等的实数根;
④将x-1替换x,由方程ax2+bx+c=0的两根x1=-3,x2=1,可得结论.
解:①由抛物线的对称性可知:与x轴交于另一点为(-3,0),
∴9a-3b+c=0;
故①正确;
②由图象得:当x=-2时,y>0,
∴4a-2b+c>0,
故②正确;
③∵抛物线的顶点(-1,4),
∴方程ax2+bx+c=4有两个相等的实数根,
即方程ax2+bx+c-4=0有两个相等的实数根;
故③正确;
④由题意得:方程ax2+bx+c=0的两根为:x1=-3,x2=1,
∴方程a(x-1)2+b(x-1)+c=0的两根是:x-1=-3或x-1=1,
∴x1=-2,x2=2,
故④正确;
综上得:正确结论为: 4个.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】正方形网格中,小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.下图![]() 中的正方形网格中
中的正方形网格中![]() 是格点三角形,小正方形网格的边长为
是格点三角形,小正方形网格的边长为![]() (单位长度).
(单位长度).
![]() 的面积是________(平方单位);
的面积是________(平方单位);
![]() 在图
在图![]() 所示的正方形网格中作出格点
所示的正方形网格中作出格点![]() 和
和![]() ″
″![]() ″
″![]() ″,使
″,使![]() ,
,![]() ″
″![]() ″
″![]() ″
″![]() ,且
,且![]() 、
、![]() 、
、![]() ″
″![]() ″中任意两条线段的长度都不相等;
″中任意两条线段的长度都不相等;
![]() 在所有与
在所有与![]() 相似的格点三角形中,是否存在面积为
相似的格点三角形中,是否存在面积为![]() (平方单位)的格点三角形?如果存在,请在图
(平方单位)的格点三角形?如果存在,请在图![]() 中作出,如果不存在,请说明理由.
中作出,如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形。
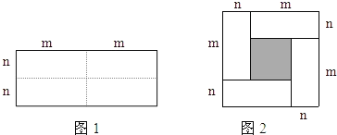
(1)请用两种不同的方法求图2中阴影部分的面积(直接用含m,n的代数式表示).
方法1:;
方法2:.
(2)根据(1)中的结论,请你写出代数式(m+n)2,(m-n)2,mn之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:已知实数a,b满足:a+b=5,ab=4,求a-b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 地将一批物资运往
地将一批物资运往![]() 地,两车离
地,两车离![]() 地的距离
地的距离![]() (千米)与其相关的时间
(千米)与其相关的时间![]() (小时)变化的图像如图所示.读图后填空:
(小时)变化的图像如图所示.读图后填空:
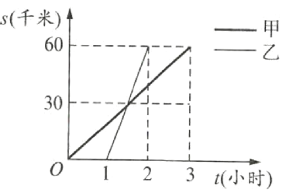
(1)![]() 地与
地与![]() 地之间的距离是______千米;
地之间的距离是______千米;
(2)甲车由![]() 地前往
地前往![]() 地时所对应的
地时所对应的![]() 与
与![]() 的函数解析式及定义域是__________;
的函数解析式及定义域是__________;
(3)甲车由![]() 地前往
地前往![]() 地比乙车由
地比乙车由![]() 地前往
地前往![]() 地多用了______小时.
地多用了______小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△OAB,△OCD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
(1)若O、C、A在一条直线上,连AD、BC,分别取AD、BC的中点M、N如图(1),求出线段MN、AC之间的数量关系;
(2)若将△OCD绕O旋转到如图(2)的位置,连AD、BC,取BC的中点M,请探究线段OM、AD之间的关系,并证明你的结论;
(3)若将△OCD由图(1)的位置绕O顺时针旋转角度α(0°<α<360°),且OA=4,OC=2,是否存在角度α使得OC⊥BC?若存在,请直接写出此时△ABC的面积;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25名同学参加比赛,成绩分别为A、B、C、D四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图,如图所示.
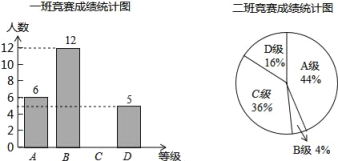
(1)把一班竞赛成绩统计图补充完整;
(2)写出下表中a、b、c的值:
平均数(分) | 中位数(分) | 众数(分) | 方差 | |
一班 | a | b | 90 | 106.24 |
二班 | 87.6 | 80 | c | 138.24 |
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
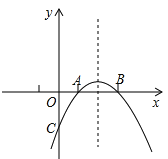
【题目】已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB=1的点P有几个?并求出所有点P的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com