
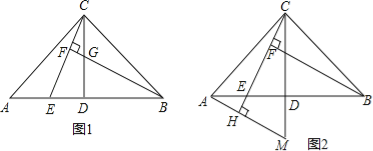
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.

【答案】(1)证明见解析(2)BE=CM.证明见解析.
【解析】试题分析:(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG,
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
(1)证明:∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
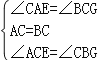
∴△AEC≌△CGB(ASA),
∴AE=CG,
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,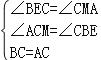 ,
,
∴△BCE≌△CAM(AAS),
∴BE=CM.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD.
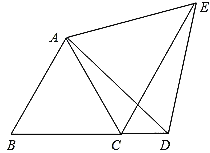
求证:(1)△ABD≌△ACE
(2)△ADE为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行全体学生“汉字听写”比赛,每位学生听写汉字49个.随机抽取了部分学生的听写结果,绘制成如下的图表.
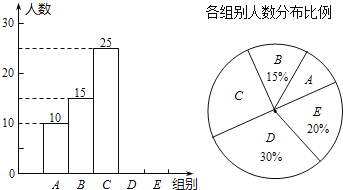
组别 | 正确字数x | 人数 |
A | 0≤x<10 | 10 |
B | 10≤x<20 | 15 |
C | 20≤x<30 | 25 |
D | 30≤x<40 | m |
E | 40≤x<50 | n |
根据以上信息完成下列问题:
(1)统计表中的m= ,n= ,并补全条形统计图;
(2)求扇形统计图中“C组”所对应的圆心角的度数;
(3)已知该校共有2400名学生,如果听写正确的汉字的个数少于30个定为不合格,请你估计该校本次听写比赛不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①,且∠α=50°,则∠1+∠2= ;
(2)若点P在斜边AB上运动,如图②,则∠α、∠1、∠2之间的关系为 ;
(3)如图③,若点P在斜边BA的延长线上运动(CE<CD),请直接写出∠α、∠1、∠2之间的关系: ;
(4)若点P运动到△ABC形外(只需研究图④情形),则∠α、∠1、∠2之间有何关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求1+2+22+23+24+…22013的值.
解:设S=1+2+22+23+24+…+22012+22013,将等式两边同时乘以2得:
2S=2+22+23+24+25+…+22013+22014,将下式减去上式得:
2S﹣S=22014﹣1,即S=22014﹣1,即1+2+22+23+24+…22013=﹣1
请你仿照此法计算1+3+32+33+34…+32014的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com