
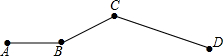
 如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是60千米/小时,BC段为上山路,车速是45千米/小时,CD段为下山路,车速是72千米/小时,已知下山路的长是上山路的2倍.
如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是60千米/小时,BC段为上山路,车速是45千米/小时,CD段为下山路,车速是72千米/小时,已知下山路的长是上山路的2倍.| 72-a |
| 3 |
| 72-a |
| 3 |
| 12 |
| 60 |
| 20 |
| 45 |
| 40 |
| 72 |
| 6 |
| 5 |
| 6 |
| 60 |
| 22 |
| 45 |
| 44 |
| 72 |
| 243 |
| 1620 |
| 72-a |
| 3 |
| a |
| 60 |
| b |
| 45 |
| 2b |
| 72 |
| 9a+12b+16b |
| 540 |
| 9a+28b |
| 540 |
9a+
| ||
| 540 |
| 2016-a |
| 1620 |


科目:初中数学 来源: 题型:
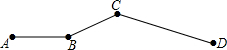 如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是30千米/小时,BC段为上山路,车速是22.5千米/小时,CD段为下山路,车速是36千米/小时,已知下山路是上山路的2倍.
如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是30千米/小时,BC段为上山路,车速是22.5千米/小时,CD段为下山路,车速是36千米/小时,已知下山路是上山路的2倍.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
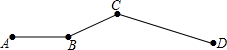 如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是30千米/小时,BC段为上山路,车速是22.5千米/小时,CD段为下山路,车速是36千米/小时,已知下山路是上山路的2倍.
如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是30千米/小时,BC段为上山路,车速是22.5千米/小时,CD段为下山路,车速是36千米/小时,已知下山路是上山路的2倍.查看答案和解析>>
科目:初中数学 来源: 题型:
如图,老王开车从A到D,全程共72千米.其中AB段为平地,车速是30千米/小时,BC段为上山路,车速是22.5千米/小时,CD段为下山路,车速是36千米/小时,已知下山路是上山路的2倍.
(1)若AB=6千米,老王开车从A到D共需多少时间?
 (2)当BC的长度在一定范围内变化时,老王开车从A到D所需时间是否会改变?为什么?(给出计算过程)
(2)当BC的长度在一定范围内变化时,老王开车从A到D所需时间是否会改变?为什么?(给出计算过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com