
Ϊ����ʵ����Ժ��ָʾ���ط�������̨��һϵ�С���ũ���Ż����ߣ�ʹũ�������������ӣ�ijũ����������һ��ũ��Ʒ����֪���ֲ�Ʒ�ijɱ���Ϊÿǧ��20Ԫ���г����鷢�֣��ò�Ʒÿ���������y(ǧ��)�����ۼ�x(Ԫ/ǧ��)�����¹�ϵ�� . �����ֲ�Ʒÿ�����������ΪwԪ.
. �����ֲ�Ʒÿ�����������ΪwԪ.
��1����w��x֮��ĺ�����ϵʽ��
��2���ò�Ʒ���ۼ۶�Ϊÿǧ�˶���Ԫʱ��ÿ����������������������Ƕ���Ԫ��
��1��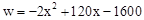 ����2���ò�Ʒ���ۼ۶�Ϊÿǧ��30Ԫʱ��ÿ������������������������200Ԫ.
����2���ò�Ʒ���ۼ۶�Ϊÿǧ��30Ԫʱ��ÿ������������������������200Ԫ.
���������������1���������۶�=�����������ۼ۵�x���г�������ϵʽ����2�����䷽������2���ĺ�����ϵʽ���Σ����ö��κ��������������ֵ.
�����������1��������ã� ��
��
��w��x�ĺ�����ϵʽΪ��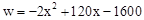 .
.
��2�� ��
��
�ߩ�2��0���൱x=30ʱ��w�����ֵ��w���ֵΪ200.
�𣺸ò�Ʒ���ۼ۶�Ϊÿǧ��30Ԫʱ��ÿ������������������������200Ԫ.
���㣺1.���κ�����Ӧ�ã�2.��ʵ�������к�����ϵʽ��3.���κ�������ֵ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij��Ʒ�Ľ���Ϊÿǧ��40Ԫ�����۵��������������Ĺ�ϵ���±���ÿǧ���ۼ۲��ܸ���65Ԫ����
| ���۵���(Ԫ) | 50 | 53 | 56 | 59 | 62 | 65 |
| ����������ǧ�ˣ� | 420 | 360 | 300 | 240 | 180 | 120 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ��������ABCD�У�AD��BC����B��90�㣬BC��6��AD��3��
��DCB��30��.��E��Fͬʱ��B�������������BC���������ƶ�.��֪F���ƶ��ٶ���E���ƶ��ٶȵ�2������EFΪһ����CB���Ϸ����ȱߡ�EFG����E���ƶ�����Ϊx��x��0��.
�š�EFG�ı߳���___________ ���ú���x�Ĵ���ʽ��ʾ������x��2ʱ����G��λ����_______��
������EFG������ABCD�ص����������y����
�ٵ�0��x��2ʱ��y��x֮��ĺ�����ϵʽ��
�ڵ�2��x��6ʱ��y��x֮��ĺ�����ϵʽ��
��̽����еõ��ĺ���y��xȡ����ֵʱ���������ֵ����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������� ��x�ύ��A��B���㣬��y�ύ��C�㣬�ı���OBHCΪ���Σ�CH���ӳ��߽��������ڵ�D��5��2��������BC��AD.
��x�ύ��A��B���㣬��y�ύ��C�㣬�ı���OBHCΪ���Σ�CH���ӳ��߽��������ڵ�D��5��2��������BC��AD.
��1����C������꼰�����ߵĽ���ʽ����6�֣�
��2������BCH�Ƶ�B��˳ʱ����ת90�������x����۵õ���BEF����C���E��Ӧ�����жϵ�E�Ƿ������������ϣ���˵�����ɣ���4�֣�
��3�������E��ֱ�߽�AB���ڵ�P����CD���ڵ�Q.���Ƿ���ڵ�P��ʹֱ��PQ������ABCD�����Ϊ1��3�����֣������ڣ����P�����ꣻ�������ڣ���˵������. ��4�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�̳�����һ�ֽ���Ϊ20Ԫ/̨��̨�ƣ������鷢�֣���̨��ÿ���������W��̨�������۵���x��Ԫ������W=-2x+80������������̨��ÿ�������Ϊy��Ԫ������y��x֮��ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ�����ͼ���㣨0����4�����ҵ�x=2�������ֵ��2����ö��κ����Ĺ�ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��֪���κ�����ͼ���� Ϊ���㣬�ҹ���
Ϊ���㣬�ҹ��� ��
��
��1����ö��κ����Ľ���ʽ��
��2����ö��κ���ͼ����������Ľ������ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�������߾���A����1��0����B��5��0����C��0�� �����㣮
�����㣮
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ�������һ��P��ʹPA+PC��ֵ��С�����P�����ꣻ
��3����MΪx����һ���㣬�����������Ƿ����һ��N��ʹ��A��C��M��N�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com