B
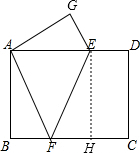
分析:如图,过点E作EH⊥BC于H,根据轴对称的性质就可以求出AG=CD,AF=CF,GE=DE,∠G=∠D=90°,∠GAF=∠C=90°.由矩形的性质和勾股定理就可以求出DE,再由△ABF∽△AGE,就可以求出BF的值,在Rt△FHE中由勾股定理就可以求出EF的值.
解答:如图,过点E作EH⊥BC于H,
∴∠EHC=∠EHF=90°.
∵四边形ABCD是矩形,
∴∠B=∠C=∠D=∠BAD=90°,AB=CD,AD=BC,
∵AB=3,BC=4,
∴CD=3,AD=4
∴∠EHC=∠C=∠D=90°,
∴四边形EHCD是矩形,
∴EH=CD,ED=CH.
∵四边形AFEG与四边形CFED关于EF对称,
∴四边形AFEG≌四边形CFED
∴AG=CD=3,AF=CF,GE=DE,∠G=∠D=90°,∠GAF=∠C=90°.
设ED=x,则GE=x,AE=4-x,在Rt△AGE中,由勾股定理,得
9+x
2=(4-x)
2,
解得:x=

,
∴AE=

.
∵∠GAE+∠FAE=∠FAE+∠BAF=90°,
∴∠GAE=∠BAF.
∵∠G=∠B=90°,
∴△ABF∽△AGE,
∴
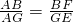
,
∴
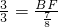
,
∴BF=

.
∴FH=4-

-

=

.
在Rt△FHE中,由勾股定理,得
EF=

.
故选B.
点评:本题考查了轴对称的性质的运用,勾股定理的运用,矩形的判定及性质的运用,解答时灵活运用勾股定理求解是关键.

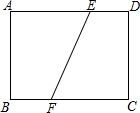 如图,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使点C与点A重合,则折痕EF的长为
如图,长方形ABCD中,AB=3,BC=4,若将该矩形折叠,使点C与点A重合,则折痕EF的长为
 ,
, .
.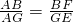 ,
,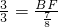 ,
, .
. -
- =
= .
. .
.

 如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)
如图,长方形ABCD中放置9个形状、大小都相同的小长方形,小长方形的长为x,宽为y(尺寸如图)