
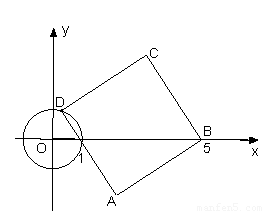
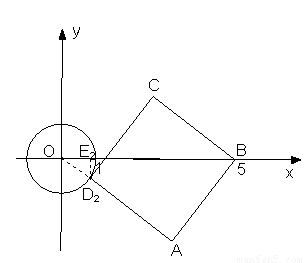
如图,⊙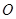 的半径为
的半径为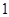 ,正方形
,正方形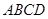 顶点
顶点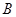 坐标为
坐标为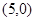 ,顶点
,顶点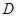 在⊙
在⊙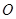 上运动.
上运动.
(1)当点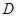 运动到与点
运动到与点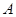 、
、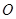 在同一条直线上时,试证明直线
在同一条直线上时,试证明直线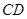 与⊙
与⊙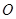 相切;
相切;
(2)当直线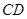 与⊙
与⊙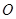 相切时,求
相切时,求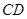 所在直线对应的函数关系式;
所在直线对应的函数关系式;
(3)设点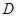 的横坐标为
的横坐标为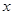 ,正方形
,正方形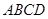 的面积为
的面积为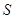 ,求
,求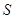 与
与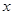 之间的函数关系式,并求出
之间的函数关系式,并求出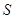 的最大值与最小值.
的最大值与最小值.
解:(1) ∵四边形 为正方形 ∴
为正方形 ∴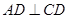
∵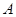 、
、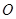 、
、 在同一条直线上 ∴
在同一条直线上 ∴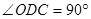 ∴直线
∴直线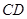 与⊙
与⊙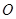 相切;
相切;
(2)直线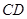 与⊙
与⊙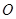 相切分两种情况:
相切分两种情况:
①如图1, 设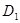 点在第二象限时,过
点在第二象限时,过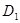 作
作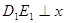 轴于点
轴于点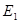 ,
,

设此时的正方形的边长为 ,则
,则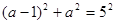 ,解得
,解得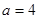 或
或 (舍去).
(舍去).
由 ∽
∽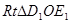 得
得
∴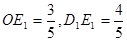 ∴
∴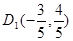 ,故直线
,故直线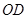 的函数关系式为
的函数关系式为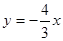 ;
;
②如图2, 设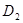 点在第四象限时,过
点在第四象限时,过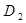 作
作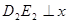 轴于点
轴于点 ,
,
设此时的正方形的边长为 ,则
,则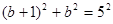 ,解得
,解得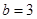 或
或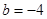 (舍去).
(舍去).
由 ∽
∽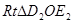 得
得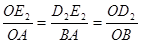
∴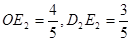 ∴
∴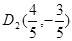 ,故直线
,故直线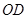 的函数关系式为
的函数关系式为 .
.
(3)设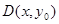 ,则
,则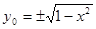 ,由
,由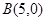 得
得
∴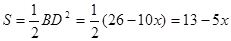
∵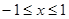
∴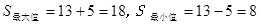 .
.
【解析】(1)由题意得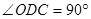 ,即直线
,即直线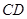 与⊙
与⊙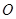 相切;
相切;
(2)分两种情况:①如图1, 设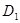 点在第二象限时,过
点在第二象限时,过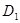 作
作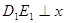 轴于点
轴于点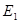 ,根据勾股定理及相似三角形对应边成比例即得结果;②如图2, 设
,根据勾股定理及相似三角形对应边成比例即得结果;②如图2, 设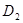 点在第四象限时,过
点在第四象限时,过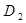 作
作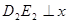 轴于点
轴于点 ,根据勾股定理及相似三角形对应边成比例即得结果;
,根据勾股定理及相似三角形对应边成比例即得结果;
(3)设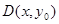 ,则
,则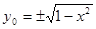 ,由
,由 得
得
则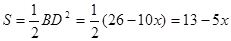 ,再根据x的范围即得结果。
,再根据x的范围即得结果。


科目:初中数学 来源: 题型:
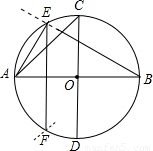
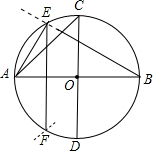 如图,⊙O的半径为1,如果作两条互相垂直的直径AB,CD,那么弦AC是⊙O的内接正四边形的一条边.若以A为圆心,以1为半径画弧,弧与⊙O相交于点E,F,则弦EC是⊙O的内接正十二边形的一条边,EC的长为( )
如图,⊙O的半径为1,如果作两条互相垂直的直径AB,CD,那么弦AC是⊙O的内接正四边形的一条边.若以A为圆心,以1为半径画弧,弧与⊙O相交于点E,F,则弦EC是⊙O的内接正十二边形的一条边,EC的长为( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知半径为1的⊙O1与x轴交于A,B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一张半径为1的图形纸片在边长为a(a>2)的正五边形内任意移动,如果这张圆形纸片在正五边形内不能接触到的部分用阴影表示,则下列示意图中表示正确的是( )
如图,一张半径为1的图形纸片在边长为a(a>2)的正五边形内任意移动,如果这张圆形纸片在正五边形内不能接触到的部分用阴影表示,则下列示意图中表示正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 如图,⊙O的半径为1,如果作两条互相垂直的直径AB,CD,那么弦AC是⊙O的内接正四边形的一条边.若以A为圆心,以1为半径画弧,弧与⊙O相交于点E,F,则弦EC是⊙O的内接正十二边形的一条边,EC的长为
如图,⊙O的半径为1,如果作两条互相垂直的直径AB,CD,那么弦AC是⊙O的内接正四边形的一条边.若以A为圆心,以1为半径画弧,弧与⊙O相交于点E,F,则弦EC是⊙O的内接正十二边形的一条边,EC的长为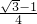



查看答案和解析>>
科目:初中数学 来源:2009年中考数学模拟检测试卷(1)(解析版) 题型:选择题
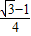
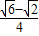
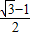
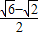
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com