
 如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=$\frac{1}{2}$∠A.
如图,在△ABC中,∠C=90°,D、F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE=$\frac{1}{2}$∠A.分析 (1)首先连接OE,由在△ABC中,∠C=90°,FG⊥BC,可得FG∥AC,又由∠OFE=$\frac{1}{2}$∠A,易得EF平分∠BFG,继而证得OE∥FG,证得OE⊥BC,则可得BC是⊙O的切线;
(2)由在△OBE中,sinB=$\frac{3}{5}$,⊙O的半径为r,可求得OB,BE的长,然后由在△BFG中,求得BG,FG的长,则可求得EG的长,易证得△EGH∽△FGE,然后由相似三角形面积比等于相似比的平方,求得答案.
解答 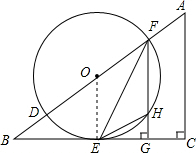 (1)证明:连接OE,
(1)证明:连接OE,
∵在△ABC中,∠C=90°,FG⊥BC,
∴∠BGF=∠C=90°,
∴FG∥AC,
∴∠OFG=∠A,
∴∠OFE=$\frac{1}{2}$∠OFG,
∴∠OFE=∠EFG,
∵OE=OF,
∴∠OFE=∠OEF,
∴∠OEF=∠EFG,
∴OE∥FG,
∴OE⊥BC,
∴BC是⊙O的切线;
(2)解:∵在Rt△OBE中,sinB=$\frac{3}{5}$,⊙O的半径为r,
∴OB=$\frac{5}{3}$r,BE=$\frac{4}{3}$r,
∴BF=OB+OF=$\frac{8}{3}$r,
∴FG=BF•sinB=$\frac{8}{5}$r,
∴BG=$\sqrt{B{F}^{2}-F{G}^{2}}$=$\frac{32}{15}$r,
∴EG=BG-BE=$\frac{4}{5}$r,
∴S△FGE=$\frac{1}{2}$EG•FG=$\frac{16}{25}$r2,EG:FG=1:2,
∵BC是切线,
∴∠GEH=∠EFG,
∵∠EGH=∠FGE,
∴△EGH∽△FGE,
∴$\frac{{S}_{△EGH}}{{S}_{△FGE}}$=($\frac{EG}{FG}$)2=$\frac{1}{4}$,
∴S△EHG=$\frac{1}{4}$S△FGE=$\frac{4}{25}$r2.
点评 此题考查了切线的判定、相似三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-3,0)、B(5,0)、C(0,5)三点,O为坐标原点
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-3,0)、B(5,0)、C(0,5)三点,O为坐标原点查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 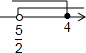 | B. | 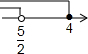 | C. | 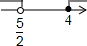 | D. | 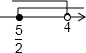 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
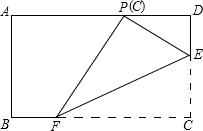 如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=2$\sqrt{3}$a.
如图,在矩形ABCD中,点E、F分别在边CD、BC上,且DC=3DE=3a.将矩形沿直线EF折叠,使点C恰好落在AD边上的点P处,则FP=2$\sqrt{3}$a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≤2 | B. | x>1 | C. | 1<x≤2 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运行区间 | 成人票价(元/张) | 学生票价(元/张) | ||
| 出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
| 南靖 | 厦门 | 26 | 22 | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com