

分析 连接OA,作OC⊥弦AB,
(1)当一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道时,OC=3-2=1,在直角△AOC中利用勾股定理求得AC的长,进而求得AB与2.3米进行比较;
(2)高度4m,宽为2.3m的大货车正好能顺利通过这个隧道时,在直角△AOC中,利用定理求得OA即可.
解答 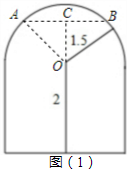 解:(1)当一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道时,
解:(1)当一辆高3m,宽2.3m的集装箱卡车能顺利通过这个隧道时,
OC=3-2=1,
连接OA,作OC⊥弦AB,在直角△AOC中,AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{1.{5}^{2}-{1}^{2}}$=$\frac{\sqrt{5}}{2}$,
则AB=2OC=$\sqrt{5}$<2.3,则一辆高3m,宽2.3m的集装箱卡车不能顺利通过这个隧道;
(2)高度4m,宽为2.3m的大货车正好能顺利通过这个隧道时,
OC=4-2=2(m),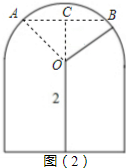
AC=$\frac{2.3}{2}$=1.15(m),
则OA=$\sqrt{A{C}^{2}+O{C}^{2}}$=$\sqrt{1.1{5}^{2}+{2}^{2}}$=$\frac{\sqrt{2129}}{20}$(m).
答:半圆拱的半径至少为$\frac{\sqrt{2129}}{20}$米.
点评 本题考查了垂径定理的应用,在圆的半径、弦长以及弦心距之间的计算常用的方法是转化为垂径定理的计算.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
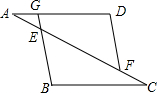 如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )
如图,点A,E,F,C在同一条直线上,AD∥BC,BE的延长线交AD于点G,且BG∥DF,则下列结论错误的是( )| A. | $\frac{AG}{AD}=\frac{AE}{AF}$ | B. | $\frac{AG}{AD}=\frac{EG}{DF}$ | C. | $\frac{AE}{AC}=\frac{AG}{AD}$ | D. | $\frac{AD}{BC}=\frac{DF}{BE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9a2-4b2=(3a-2b)2 | B. | -3ab2+6ab=-3ab(b+2) | ||
| C. | $\frac{1}{2}$a2-ab+$\frac{1}{2}$b2=$\frac{1}{2}$(a-b)2 | D. | -a2-b2=-(a+b)(a-b) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 阶梯 | 电量 | 电价 |
| 一档 | 0-180度 | 0.6元/度 |
| 二档 | 181-400度 | 二档电价 |
| 三档 | 401度及以上 | 三档电价 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com