
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据已知条件“a>0,b<0,c>0”判断出该函数图象的开口方向、与x和y轴的交点、对称轴所在的位置,然后据此来判断它的图象一定不经过第三象限.
解答 解:①∵a>0、c>0,
∴该抛物线开口方向向上,且与y轴交于正半轴;
②∵a>0,b<0,
∴二次函数y=ax2+bx+c的函数图象的对称轴是x=-$\frac{b}{a}$>0,
∴二次函数y=ax2+bx+c的函数图象的对称轴在第一象限;
综合①②,二次函数y=ax2+bx+c的图象一定不经过第三象限.
故选C.
点评 本题考查了二次函数图象与系数的关系.根据二次函数y=ax2+bx+c系数符号判断抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数.


科目:初中数学 来源: 题型:解答题
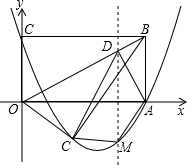 如图,矩形OABC中,OA=10,OC=5,将其沿对角线OB对折,点C落到点C′处,以点O为坐标原点,OA、OC所在直线为坐标轴,建立如图所示的平面直角坐标系.
如图,矩形OABC中,OA=10,OC=5,将其沿对角线OB对折,点C落到点C′处,以点O为坐标原点,OA、OC所在直线为坐标轴,建立如图所示的平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1000 | B. | 1500 | C. | 1800 | D. | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A′处,折痕为MN,点N在AD边上.
如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A′处,折痕为MN,点N在AD边上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校六年级四个班级向希望工程捐款数额的统计图,回答下面问题:
某校六年级四个班级向希望工程捐款数额的统计图,回答下面问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.1 (精确到0.1) | B. | 0.06 (精确到千分位) | ||
| C. | 0.06 (精确到百分位) | D. | 0.0602 (精确到0.0001) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com