
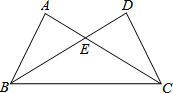
 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC. 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:初中数学 来源: 题型:
| A、(-p2q)3=-p5q3 |
| B、(12a2b3c)÷(6ab2)=2ab |
| C、3m2÷(3m-1)=m-3m2 |
| D、(x2-4x)÷x=x-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 月用水量(吨) | 3 | 4 | 5 | 7 | 8 | 9 | 40 |
| 户数 | 4 | 3 | 5 | 11 | 4 | 2 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在所给网格图中每小格均为边长是1的正方形.△ABC的顶点均在格点上.请完成下列各题:(用直尺画图)
如图,在所给网格图中每小格均为边长是1的正方形.△ABC的顶点均在格点上.请完成下列各题:(用直尺画图)查看答案和解析>>
科目:初中数学 来源: 题型:
 已知点A与点B (-1,1)关于x轴对称,点C在y轴的负半轴上,且到原点的距离为2,一直线经过点A和点C.
已知点A与点B (-1,1)关于x轴对称,点C在y轴的负半轴上,且到原点的距离为2,一直线经过点A和点C.查看答案和解析>>
科目:初中数学 来源: 题型:
 某航船以20海里/时的速度向正北方向航行,在A处看灯塔Q在航船北偏东45°处,半小时后航行到B处,此时灯塔Q与航船的距离最短.
某航船以20海里/时的速度向正北方向航行,在A处看灯塔Q在航船北偏东45°处,半小时后航行到B处,此时灯塔Q与航船的距离最短.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com