Question

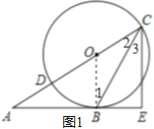
【题目】（12分）如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．

（1）求证：CB平分∠ACE；

（2）若BE=3，CE=4，求⊙O的半径．

Answer 1

【答案】

【解析】试题分析：（1）证明：如图1，连接OB，由AB是⊙0的切线，得到OB⊥AB，由于CE丄AB，的OB∥CE，于是得到∠1=∠3，根据等腰三角形的性质得到∠1=∠2，通过等量代换得到结果．

（2）如图2，连接BD通过△DBC∽△CBE，得到比例式，列方程可得结果．

（1）证明：如图1，连接OB，

∵AB是⊙0的切线，

∴OB⊥AB，

∵CE丄AB，

∴OB∥CE，

∴∠1=∠3，

∵OB=OC，

∴∠1=∠2，

∴∠2=∠3，

∴CB平分∠ACE；

（2）如图2，连接BD，

∵CE丄AB，

∴∠E=90°，

∴BC===5，

∵CD是⊙O的直径，

∴∠DBC=90°，

∴∠E=∠DBC，

∴△DBC∽△CBE，

∴，

∴BC2=CDCE，

∴CD==，

∴OC==，

∴⊙O的半径=．