
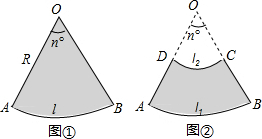
分析 (1)根据扇形公式之间的关系,结合已知条件推出结果即可;
(2)求出l1+l2=40-2h,代入(1)的结果,化成顶点式,即可得出答案.
解答 (1)S扇环=$\frac{1}{2}$(l1+l2)h,
证明:设大扇形半径为R,小扇形半径为r,圆心角度数为n,则由l=$\frac{nπr}{180}$,得R=$\frac{180{l}_{1}}{nπ}$,r=$\frac{180{l}_{2}}{nπ}$
所以图中扇环的面积S=$\frac{1}{2}$×l1×R-$\frac{1}{2}$×l2×r
=$\frac{1}{2}$l1•$\frac{180{l}_{1}}{nπ}$-$\frac{1}{2}$l2•$\frac{180{l}_{2}}{nπ}$
=$\frac{90}{nπ}$(l12-l22)
=$\frac{90}{nπ}$(l1+l2)(l1-l2)
=$\frac{1}{2}$•$\frac{180}{nπ}$•($\frac{nπ}{180}$R+$\frac{nπ}{180}$r)(l1-l2)
=$\frac{1}{2}$(l1+l2)(R-r)
=$\frac{1}{2}$(l1+l2)h,
故猜想正确.
(2)解:根据题意得:l1+l2=40-2h,
则S扇环=$\frac{1}{2}$(l1+l2)h
=$\frac{1}{2}$(40-2h)h
=-h2+20h
=-(h-10)2+100
∵-1<0,
∴开口向下,有最大值,
当h=10时,最大值是100,
即线段AD的长h为10m时,花园的面积最大,最大面积是100m2.
点评 本题主要考查了扇形面积公式,弧长公式,二次函数的顶点式的应用,能猜想出正确结论是解此题的关键,有一定的难度.


科目:初中数学 来源: 题型:解答题
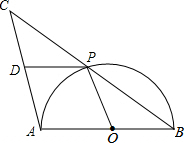 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
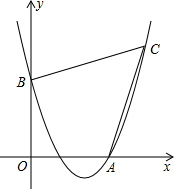 如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).
如图,已知抛物线经过点A(4,0),B(0,4),C(6,6).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 24cm | B. | 48cm | C. | 96cm | D. | 192cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com