
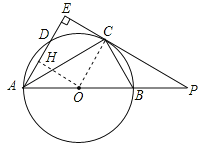
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
【答案】(1)证明见试题解析;(2)AB=3PB,理由见试题解析;(3)5.
【解析】
试题分析:(1)首先连接OC,由PE是⊙O的切线,AE和过点C的切线互相垂直,可证得OC∥AE,又由OA=OC,易证得∠DAC=∠OAC,即可得AC平分∠BAD;
(2)由AB是⊙O的直径,PE是切线,可证得∠PCB=∠PAC,即可证得△PCB∽△PAC,然后由相似三角形的对应边成比例与PB:PC=1:2,即可求得答案;
(3)首先过点O作OH⊥AD于点H,则AH=![]() AD=
AD=![]() ,四边形OCEH是矩形,即可得AE=
,四边形OCEH是矩形,即可得AE=![]() +OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案.
+OC,由OC∥AE,可得△PCO∽△PEA,然后由相似三角形的对应边成比例,求得OC的长,再由△PBC∽△PCA,证得AC=2BC,然后在Rt△ABC中,AC2+BC2=AB2,可得(2BC)2+BC2=52,即可求得BC的长,继而求得答案.
试题解析:(1)连接OC,∵PE是⊙O的切线,∴OC⊥PE,∵AE⊥PE,∴OC∥AE,∴∠DAC=∠OCA,∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OAC,∴AC平分∠BAD;
(2)线段PB,AB之间的数量关系为:AB=3PB.理由:
∵AB是⊙O的直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°,∵OB=OC,∴∠OCB=∠ABC,∵∠PCB+∠OCB=90°,∴∠PCB=∠PAC,∵∠P是公共角,∴△PCB∽△PAC,∴![]() ,∴
,∴![]() =PBPA,∵PB:PC=1:2,∴PC=2PB,∴PA=4PB,∴AB=3PB;
=PBPA,∵PB:PC=1:2,∴PC=2PB,∴PA=4PB,∴AB=3PB;
(3)过点O作OH⊥AD于点H,则AH=![]() AD=
AD=![]() ,四边形OCEH是矩形,∴OC=HE,∴AE=
,四边形OCEH是矩形,∴OC=HE,∴AE=![]() +OC,∵OC∥AE,∴△PCO∽△PEA,∴
+OC,∵OC∥AE,∴△PCO∽△PEA,∴![]() ,∵AB=3PB,AB=2OB,∴OB=
,∵AB=3PB,AB=2OB,∴OB=![]() PB,∴
PB,∴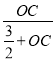 =
=![]() =
=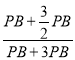 ,∴OC=
,∴OC=![]() ,∴AB=5,∵△PBC∽△PCA,∴
,∴AB=5,∵△PBC∽△PCA,∴![]() ,∴AC=2BC,在Rt△ABC中,
,∴AC=2BC,在Rt△ABC中,![]() ,∴
,∴![]() ,∴BC=
,∴BC=![]() ,∴AC=
,∴AC=![]() ,∴S△ABC=
,∴S△ABC=![]() ACBC=5.
ACBC=5.


科目:初中数学 来源: 题型:
【题目】如图,四边形 ![]() 是正方形,
是正方形, ![]() 是
是 ![]() 垂直平分线上的点,点
垂直平分线上的点,点 ![]() 关于
关于 ![]() 的对称点是
的对称点是 ![]() ,直线
,直线 ![]() 与直线
与直线 ![]() 交于点
交于点 ![]() .
.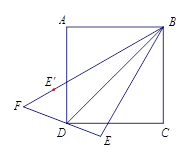
(1)若点 ![]() 是
是 ![]() 边的中点,连接
边的中点,连接 ![]() ,则
,则 ![]() =;
=;
(2)小明从老师那里了解到,只要点 ![]() 不在正方形的中心,则直线
不在正方形的中心,则直线 ![]() 与
与 ![]() 所夹锐角不变.他尝试改变点
所夹锐角不变.他尝试改变点 ![]() 的位置,计算相应角度,验证老师的说法.
的位置,计算相应角度,验证老师的说法.
如图,将点 ![]() 选在正方形内,且△
选在正方形内,且△ ![]() 为等边三角形,求出直线
为等边三角形,求出直线 ![]() 与
与 ![]() 所夹锐角的度数;
所夹锐角的度数;
(3)请你继续研究这个问题,可以延续小明的想法,也可用其它方法.
我选择小明的想法;并简述求直线 ![]() 与
与 ![]() 所夹锐角度数的思路.
所夹锐角度数的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c为平面上三条不同直线,
(1)若a∥b,b∥c,则a与c的位置关系是________;
(2)若a⊥b,b⊥c,则a与c的位置关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE;

(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:
﹣2,4,﹣8,16,﹣32,64,…
﹣1,3,﹣7,17,﹣31,65,…
﹣![]() ,1,﹣2,4,﹣8,16…
,1,﹣2,4,﹣8,16…
(1)第①行数按什么规律排列?
(2)第②、③与第①行数分别有什么关系?
(3)取每行的第10个数,计算这三个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校初一某班学生的平均体重是45公斤.
(1)下表给出了该班6位同学的体重情况(单位:公斤),完成下表
姓 名 | 小丽 | 小华 | 小明 | 小方 | 小颖 | 小宝 |
体 重 | 37 | 50 | 40 |
| 36 | 48 |
体重与平均体重的差值 | ﹣8 | +5 |
| +2 |
|
|
(2)最重的与最轻的同学的体重相差多少?
(3)这6位同学的平均体重是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( ) 
A.当AB=BC时,它是菱形
B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形
D.当AC=BD时,它是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的偶数2,4,6,8…排列成如下的数表用十字框框出5个数(如图)
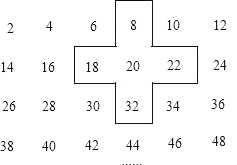
(1)十字框框出5个数的和与框子正中间的数20有什么关系?
(2)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】采摘茶叶是茶农一项很繁重的劳动,利用单人便携式采茶机能大大提高生产效率.实践证明,一台采茶机每天可采茶60公斤,是人手工采摘的5倍,购买一台采茶机需2400元.茶园雇人采摘茶叶,按每采摘1公斤茶叶m元的标准支付雇工工资,一个雇工手工采摘茶叶20天获得的全部工钱正好购买一台采茶机.
(1)求m的值;
(2)有两家茶叶种植户王家和顾家均雇人采摘茶叶,王家雇用的人数是顾家的2倍.王家所雇的人中有![]() 的人自带采茶机采摘,
的人自带采茶机采摘, ![]() 的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
的人手工采摘,顾家所雇的人全部自带采茶机采摘.某一天,王家付给雇工的工资总额比顾家付给雇工的工资总额少600元.问顾家当天采摘了多少公斤茶叶?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com