
【题目】观察下列三行数:
﹣2,4,﹣8,16,﹣32,64,…
﹣1,3,﹣7,17,﹣31,65,…
﹣![]() ,1,﹣2,4,﹣8,16…
,1,﹣2,4,﹣8,16…
(1)第①行数按什么规律排列?
(2)第②、③与第①行数分别有什么关系?
(3)取每行的第10个数,计算这三个数的和.
【答案】(1)(﹣2)n;(2)(﹣2)n+1,(﹣2)n×![]() ;(3)9×28+1.
;(3)9×28+1.
【解析】试题分析:(1)根据已知数据都是2的乘方得到,再利用第奇数个系数为负数即可得出答案;
(2)根据3行数据关系分别分析得出即可;
(3)分别求出每行第10个数进而求出它们的和.
试题解析:解:(1)∵﹣2,4,﹣8,16,﹣32,64,…
∴第一行的数是按(﹣2)n排列的;
(2)第二行的数是(﹣2)n+1,第三行的数是(﹣2)n×![]() ;
;
(3)第一行的第10个数是(﹣2)10;第一行的第10个数是(﹣2)10+1;第一行的第10个数是(﹣2)10×![]() ;所以(﹣2)10+(﹣2)10+1+(﹣2)10×
;所以(﹣2)10+(﹣2)10+1+(﹣2)10×![]() =9×28+1.
=9×28+1.


科目:初中数学 来源: 题型:
【题目】2017年国庆节放假八天,高速公路免费通行,各地风景区游人如织.其中闻名于世的北京故宫在10月1日的游客人数就已经达到了7万人,接下来的七天中,每天的游客人数变化(单位:万人)如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
(1)10月3日的人数为万人;
(2)这八天,游客人数最多的是10月日,达到万人;游客人数最少的是10月日,为万人;
(3)这8天参观故宫的总人数约为万人(结果精确到万位)
(4)如果你们一家人打算在下一个国庆节参观故宫,请你对你们的出行日期提一个建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
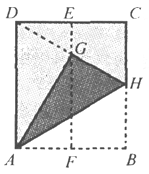
A. 2cm B. ![]() cm C. 4cm D.
cm C. 4cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
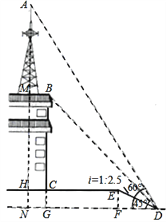
【题目】如图,某校少年宫数学课外活动初三小组的同学为测量一座铁塔AM的高度如图,他们在坡度是i=1:2.5的斜坡DE的D处,测得楼顶的移动通讯基站铁塔的顶部A和楼顶B的仰角分别是60°、45°,斜坡高EF=2米,CE=13米,CH=2米。大家根据所学知识很快计算出了铁塔高AM。亲爱的同学们,相信你也能计算出铁塔AM的高度!请你写出解答过程。(数据![]() ≈1.41,
≈1.41, ![]() ≈1.73供选用,结果保留整数)
≈1.73供选用,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程 ![]()
![]() 满足
满足 ![]() ,那么我们称这个方程为“阿凡达”方程,已知
,那么我们称这个方程为“阿凡达”方程,已知 ![]() 是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
是“阿凡达”方程,且有两个相等的实数根,则下列结论正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC,PB:PC=1:2.

(1)求证:AC平分∠BAD;
(2)探究线段PB,AB之间的数量关系,并说明理由;
(3)若AD=3,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,在平面直角坐标系中,抛物线![]() 与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在
与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在![]() 轴上且AD为⊙M的直径.点E是⊙M与
轴上且AD为⊙M的直径.点E是⊙M与![]() 轴的另一个交点,过劣弧
轴的另一个交点,过劣弧![]() 上的点F作FH⊥AD于点H,且FH=1.5.
上的点F作FH⊥AD于点H,且FH=1.5.

(1)求点D的坐标及该抛物线的表达式;
(2)若点P是![]() 轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使⊿QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角△ABC中,∠ABC=90°,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,且∠A=∠PDB.
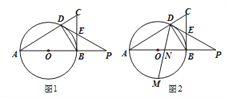
(1)求证:PD是⊙O的切线;
(2)如图2,点M是![]() 的中点,连接DM,交AB于点N,若tan∠A=
的中点,连接DM,交AB于点N,若tan∠A=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com