
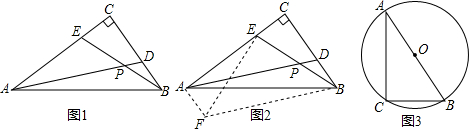
分析 (1)利用平行四边形的判定与性质得出AF=BD,进而得出△AEF≌△CBE(SAS),即可得出:∠APE的度数;
(2)根据题意首先得出△AEF∽△CBE,进而得出tan∠FBE=$\frac{EF}{BE}$=$\frac{1}{2}$,即可求出sin∠APE的值.
解答 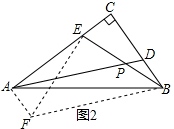 解:(1)如图2,过点B作BF∥AD且BF=AD,连接EF,AF,
解:(1)如图2,过点B作BF∥AD且BF=AD,连接EF,AF,
∵BF∥AD且BF=AD,
∴四边形AFBD是平行四边形,
∴AF=BD,
在△AEF和△CBE中
∵$\left\{\begin{array}{l}{AE=BC}\\{∠FAE=∠C}\\{AF=EC}\end{array}\right.$,
∴△AEF≌△CBE(SAS),
∴EF=BE,∠AEF+∠CEB=90°,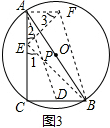
∴∠EBF=45°,
∵AD∥BF,
∴∠APE=45°;
故答案为:45°;
(2)如图3,过点B作FB∥AD且FB=AD,连接EF和AF,
∴四边形AFBD是平行四边形,
∠APE=∠FBE,AF=DB,
∵AB是⊙O直径,∴∠C=90°,
∴∠FAE=∠BCE=90°,
∵CE=2BD,BC=2AE,
∴CE=2AF,∴$\frac{CE}{AF}$=$\frac{BC}{EA}$=2,
∴△AEF∽△CBE,
∴$\frac{EF}{BE}$=$\frac{1}{2}$,∠1=∠3,
又∵∠2+∠3=90°,
∴∠1+∠2=90°,即∠FEB=90°,
在Rt△BEF中,∠FEB=90°,
∴tan∠FBE=$\frac{EF}{BE}$=$\frac{1}{2}$,
又∵∠APE=∠FBE,
∴sin∠APE=$\frac{\sqrt{5}}{5}$.
点评 此题主要考查了平行四边形的性质与判定以及全等三角形的判定与性质和相似三角形的判定与性质等知识,做出正确辅助线构造平行四边形是解题关键.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3.
如图,给正五边形的顶点依次编号为1,2,3,4,5.若从某一顶点开始,沿正五边形的边顺时针方向行走,顶点编号的数字是几,就走几个边长,则称这种走法为一次“移位”.如:小宇在编号为3的顶点上时,那么他应走3个边长,即从3→4→5→1为第一次“移位”,这时他到达编号为1的顶点;然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始,第2014次“移位”后,则他所处顶点的编号是3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
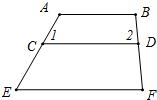 如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.
如图,下列六个条件:①∠1=∠E;②∠2=∠F;③∠A+∠1=180°;④∠B+∠2=180°;⑤∠DCE+∠E=180°;⑥∠CDF+∠F=180°,从中选取两个条件作为题设,使得命题“如果∠1=∠E,∠B+∠2=180°,那么AB∥EF”是一个真命题,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
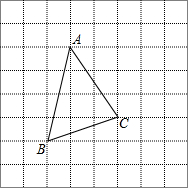 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,用一个最小的圆去覆盖△ABC,请你在如图所示的网格中,用直尺画出该圆的圆心(保留作图痕迹),并简要说明画图的方法(不要求证明)填什么.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com