
【题目】如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且AD⊥BC,垂足为F,求∠BAC的度数.
【答案】解:根据旋转的性质知,∠EAC=∠BAD=65°,∠C=∠E=70°.
如图,设AD⊥BC于点F,则∠AFB=90°,
∴在Rt△ABF中,∠B=90°﹣∠BAD=25°,
∴在△ABC中,∠BAC=180°﹣∠B﹣∠C=180°﹣25°﹣70°=85°,
即∠BAC的度数为85°.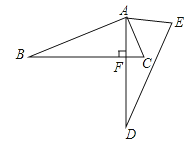
【解析】根据旋转的性质知,旋转角∠CAE=∠BAD=65°,对应角∠C=∠E=70°,则在直角△ABF中易求∠B=25°,所以利用△ABC的内角和是180°来求∠BAC的度数即可.
【考点精析】通过灵活运用三角形的内角和外角,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知:如下图, AB∥CD , 点E , F分别为AB , CD上一点.
(1)在AB , CD之间有一点M(点M不在线段EF上),连接ME , MF , 试探究∠AEM , ∠EMF , ∠MFC之间有怎样的数量关系. 请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明.
(2)如下图,在AB , CD之间有两点M , N , 连接ME , MN , NF , 请选择一个图形写出∠AEM , ∠EMN , ∠MNF , ∠NFC 存在的数量关系(不需证明).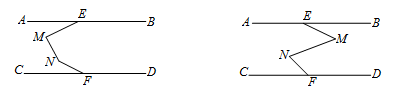
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )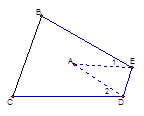
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某工程队从A点出发,沿北偏西67度方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23度的方向继续修建BC段,到达C点又改变方向,使所修路段CE∥AB,此时∠ECB有多少度?试说明理由.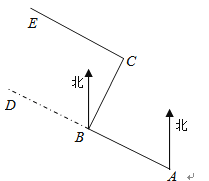
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2019年第一季度,深圳新出台的小微企业普惠性减税政策合计减税13.53亿元.“13.53亿”用科学记数法表示为( )
A. 13.53×102B. 1.353×109C. 0.1353×102D. 1.353×102
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com