
如图,一次函数y=x+b的图象与反比例函数y= 的图象交于点A和点B(﹣2,n),与x轴交于点C(﹣1,0),连接OA.
的图象交于点A和点B(﹣2,n),与x轴交于点C(﹣1,0),连接OA.
(1)求一次函数和反比例函数的解析式;
(2)若点P在坐标轴上,且满足PA=OA,求点P的坐标.
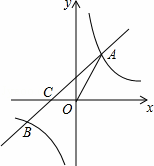
解:(1)∵一次函数y=x+b的图象与x轴交于点C(﹣1,0),
∴﹣1+b=0 ,解得b=1,
,解得b=1,
∴一次函数的解析式为y=x+1,
∵一次函数y=x+1的图象过点B(﹣2,n),
∴n=﹣2+1=﹣1,
∴B(﹣2,﹣1).
∵反比例函数y= 的图象过点B(﹣2,﹣1),
的图象过点B(﹣2,﹣1),
∴k=﹣2×(﹣1)=2,
∴反比例函数的解析式为y= ;
;
(2)由 ,解得
,解得 ,或
,或 ,
,
∵B(﹣2,﹣1),
∴A(1,2).
分两种情况:
①如果点P在x轴上,设点P的坐标为(x,0),
∵PA=OA,
∴(x﹣1)2+22=12+22,
解得x1=2,x2=0(不合题意舍去),
∴点P的坐标为(2,0);
②如果点P在y轴上,设点P的坐标为(0,y),
∵PA=OA,
∴12+(y﹣2)2=12+22,
解得y1=4,y2=0(不合题意舍去),
∴点P的坐标为(0,4);
综上所述,所求点P的坐标为(2,0)或(0,4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
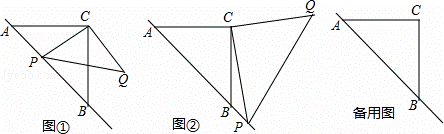
已知:△ABC是等腰三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+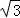 ,PA=
,PA=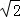 ,则:
,则:
①线段PB= 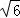 ,PC= 2 ;
,PC= 2 ;
②猜想:PA2,PB2,PQ2三者之间的数量关系为 PA2+PB2=PQ2 ;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足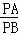 =
=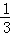 ,求
,求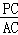 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
在一次定点投篮训练中,五位同学投中的个数分别为3,4,4,6,8,则关于这组数据的说法不正确的是( )
A.平均数是5 
 B.中位数是6 C.众数是4 D.方差是3.2
B.中位数是6 C.众数是4 D.方差是3.2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形OABC,点A,C分 别在x轴,y轴正半轴上,直线
别在x轴,y轴正半轴上,直线 交边BC于点M(m,n)(m<n),
交边BC于点M(m,n)(m<n),
 并把矩形OABC分成面积相等的两部分,过点M的双曲线
并把矩形OABC分成面积相等的两部分,过点M的双曲线 (
( )交边AB于点N.若△OAN
)交边AB于点N.若△OAN 的面积是4,求△OMN的面积.
的面积是4,求△OMN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中有三个点A(1,﹣1)、B(﹣1,﹣1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )
A. (0,0) B. (0,2) C. (2,﹣4) D. (﹣4,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com