
分析 (1)利用45度角构造等腰直角三角形△BDN,再证明四边形AEMN是矩形得到AE=MN=$\frac{1}{2}$BD即可.
(2)如图2只要证明B、F、C在以A为圆心的圆上即可以.
解答 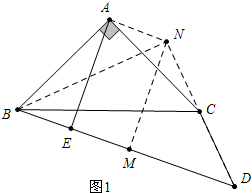 解:(1)结论:BD=2AE,理由如下:
解:(1)结论:BD=2AE,理由如下:
作BN⊥DC于N,NM⊥BD垂足为M.
∵∠BAC=90°,AB=AC,
∴BC=$\sqrt{2}$AB,
∵∠BND=90°,∠D=45°,
∴∠NBD=90°-∠D=45°,
∴∠NBD=∠D=45°,∠BND=90°,
∴$BD=\sqrt{2}$BN,
∴$\frac{BC}{AB}=\frac{BD}{BN}=\sqrt{2}$,
∵∠ABC=∠NBD=45°,
∴∠ABN=∠CBD,
∴△CBD∽△ABN,
∴∠D=∠ANB=45°,
∵∠BMN=90°,∠MBN=45°,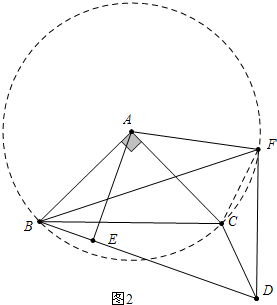
∴∠BNM=90°-∠NBM=45°,
∴∠ANM=∠ANB+∠BNM=90°,
∵AE⊥BD,
∴∠AEM=∠NME=∠ANM=90°,
∴四边形AEMN是矩形,
∴MN=AE,
∵∵∠NBD=∠D=∠BNM=∠MND=45°,
∴MN=BM=MD,
∴BD=2AE.
(2)结论:BC=$\sqrt{2}$AF,理由如下:
连接CF,∵D、F关于BC对称,
∴∠BFC=∠BDC=45°,
∵∠BAC=90°,
∴∠BAC=2∠BFC,
∴B、F、C在以A为圆心的圆上,
∴AF=AB=AC,
∵AB=AC,∠BAC=90°,
∴$BC=\sqrt{2}$AB=$\sqrt{2}$AF.
点评 本题考查等腰直角三角形的性质和判定、相似三角形的判定和性质、圆的有关知识,利用45度角添加辅助线,构造等腰直角三角形是解题的关键.


科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
画△ABC中BC边上的高,下面的画法中,正确的是 ( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的两条高BD,CE交于点F,延长CE到Q,使CQ=AB,在BD上截取BP=AC,连接AP.
如图,△ABC的两条高BD,CE交于点F,延长CE到Q,使CQ=AB,在BD上截取BP=AC,连接AP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在直角△ABC中,∠C=90°,DE⊥AC于E,交AB于D.
在直角△ABC中,∠C=90°,DE⊥AC于E,交AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,AC=30cm,BC=25cm.动点P从点C出发,沿CA方向运动,速度是2cm/s;动点Q从点B出发,沿BC方向运动,速度是1cm/s.几秒后P、Q两点相距25cm?
如图,在△ABC中,∠C=90°,AC=30cm,BC=25cm.动点P从点C出发,沿CA方向运动,速度是2cm/s;动点Q从点B出发,沿BC方向运动,速度是1cm/s.几秒后P、Q两点相距25cm?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com