练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
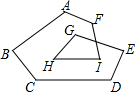
    6．如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°．

    分析 根据多边形的内角和，可得答案．

    解答 解：连EF，GI，如图，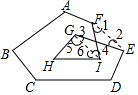
    ∵6边形ABCDEFK的内角和=（6-2）×180°=720°，
    ∴∠A+∠B+∠C+∠D+∠E+∠F=720°-（∠1+∠2），
    即∠A+∠B+∠C+∠D+∠E+∠F+（∠1+∠2）=720°，
    ∵∠1+∠2=∠3+∠4，∠5+∠6+∠H=180°，
    ∴∠A+∠B+∠C+∠D+∠E+∠F∠H+（∠3+∠4）=900°，
    ∴∠A+∠B+∠C+∠D+∠E+∠F（∠3+∠4）+∠5+∠6+∠H=720°+180°，
    ∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°，
    故答案为：900°．

    点评 本题考查了n边形的内角和定理：n边形的内角和为（n-2）×180°（n≥3的整数）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    6．解下列方程（组）：
    （1）3x-（x+4）=2（2x-1）
    （2）$\frac{y+2}{8}-\frac{y-1}{6}$=1
    （3）$\left\{\begin{array}{l}x+2y=10\\ y=-3x\end{array}$
    （4）$\left\{\begin{array}{l}3x-2y=8\\ 2x-y=5\end{array}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知$\sqrt{x+1}$+|2-y|=0，求y-x的平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

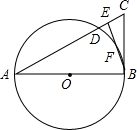    14．如图，△ABC中，E是AC上一点，且AE=AB，∠EBC=$\frac{1}{2}$∠BAC，以AB为直径的⊙O交AC于点D，交EB于点F．
    （1）求证：BC与⊙O相切；
    （2）连接BD，求∠ADB的度数；
    （3）若AB=8，sin∠EBC=$\frac{1}{4}$，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．阅读下列材料：
    正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫格点三角形．
    数学老师给小明同学出了一道题目：在图所示正方形网格（每个小正方形边长为1）中画出格点△ABC，使AB=AC=$\sqrt{5}$，BC=$\sqrt{2}$；小明同学的做法是：由勾股定理，得AB=AC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$，BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$，于是画出线段AB、AC、BC，从而画出格点△ABC．
    若△DEF中，DE=$\sqrt{17}$，EF=2$\sqrt{5}$，FD=$\sqrt{13}$，请你参考小明同学的做法，在备用图中画出△DEF，并求△DEF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．解方程组：$\left\{\begin{array}{l}{x-2y=2}\\{\frac{x}{2}-\frac{y-1}{3}=1}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．（1）计算：$\sqrt{2\frac{1}{4}}$+$\root{3}{（-4）^{3}}$×（-$\frac{1}{2}$）2
    （2）求x值：（x-2）2=25．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．目前节能灯在城市已基本普及，为响应号召，某商场计划用3800元购进甲，乙两种节能灯共120只，这两种节能灯的进价、售价如下表：
    进价（元/只）售价（元/只）
    甲型2530
    乙型4560
    （1）求甲、乙两种节能灯各进多少只？
    （2）全部售完120只节能灯后，该商场获利多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．某中学为推进素质教育，在初一年级设立了六个课外兴趣小组，如图是六个兴趣小组的频数分布直方图和扇形统计图，请根据图中提供的信息回答下列问题：
    （1）初一年级共有多少人？
    （2）补全频数分布直方图．
    （3）求“从该年级中任选一名学生，是参加音乐、科技两个小组学生”的概率．

    查看答案和解析>>

    同步练习册答案