
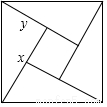
 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )| A. | ①③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 由题意$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=49}\\{(x-y)^{2}=4}\end{array}\right.$,①-②可得2xy=45记为③,①+③得到(x+y)2=94由此即可判断,
解答 解:由题意$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=49}\\{(x-y)^{2}=4}\end{array}\right.$,
①-②得2xy=45 ③,
∴2xy+4=49,
①+③得x2+2xy+y2=94,
∴(x+y)2=94,
∴①③正确,②④错误.
故选A.
点评 本题考查勾股定理,二元二次方程组等知识,解题的关键学会利用方程的思想解决问题,学会用整体恒等变形的思想,属于中考常考题型.


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:填空题
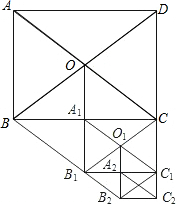 如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则${S_{平行四边形{O_1}{B_1}{B_2}{C_1}}}$=$\frac{3}{2}$.
如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则${S_{平行四边形{O_1}{B_1}{B_2}{C_1}}}$=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
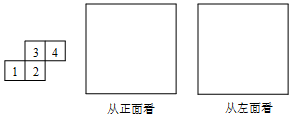 一个几何体是由几个大小相同的小立方块搭成的,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数请画出从正面、左面看到的这个几何体的形状图.
一个几何体是由几个大小相同的小立方块搭成的,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数请画出从正面、左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6cm | B. | 12cm | C. | 18cm | D. | 6cm或18cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
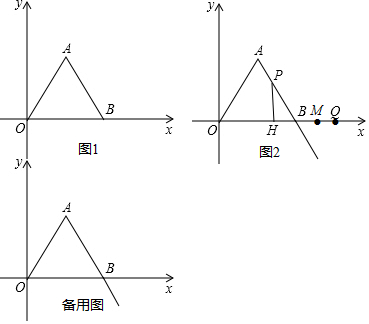
 如图,P为正方形ABCD的AD边上一点,PE⊥AD交BD于点E点,将△PCD绕C点逆时针方向旋转90°到△FCB的位置,连接PF交BD于Q点.
如图,P为正方形ABCD的AD边上一点,PE⊥AD交BD于点E点,将△PCD绕C点逆时针方向旋转90°到△FCB的位置,连接PF交BD于Q点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com