
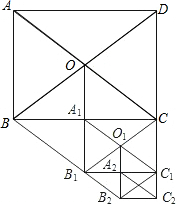
 如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则${S_{平行四边形{O_1}{B_1}{B_2}{C_1}}}$=$\frac{3}{2}$.
如图,在矩形ABCD中,AB=3,AD=4,以对角线的一半为边依次作平行四边形,则${S_{平行四边形{O_1}{B_1}{B_2}{C_1}}}$=$\frac{3}{2}$. 分析 先证明四边形OBB1C是菱形,由菱形的面积=两条对角线长积的一半,即可得出平行四边形OBB1C的面积;由矩形的面积公式得出平行四边形A1B1C1C的面积,由菱形的面积公式得出平行四边形OB1B2C的面积即可.
解答 解:∵四边形ABCD矩形,
∴OB=OC,BC=AD=4,矩形ABCD的面积=3×4=12;
∵四边形OBB1C是平行四边形,OB=OC,
∴四边形OBB1C是菱形,
∴BA1=CA1=$\frac{1}{2}$BC=2,
∴OA1是△ABC的中位线,
∴OA1=$\frac{1}{2}$AB=$\frac{3}{2}$,
∴O1B=2OA1=3,
∴平行四边形四边形OBB1C的面积=$\frac{1}{2}$×3×4=6;
根据题意得:四边形A1B1C1C是矩形,
∴平行四边形A1B1C1C=A1C×A1B1=2×$\frac{3}{2}$=3;
同理:平行四边形OB1B2C的面积=$\frac{1}{2}$×2×$\frac{3}{2}$=$\frac{3}{2}$;
故答案为:$\frac{3}{2}$.
点评 本题考查了矩形的性质、菱形的判定与性质、三角形中位线定理以及平行四边形面积的计算;熟练掌握矩形的性质,由矩形的面积公式和菱形的面积公式得出结果是解决问题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
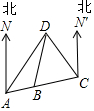 “奔跑吧,兄弟!”节目组,预设计一个新的游戏,“奔跑”需经A,B,C,D四点,如图,其中A,B,C三地在同一直线上,D点在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.
“奔跑吧,兄弟!”节目组,预设计一个新的游戏,“奔跑”需经A,B,C,D四点,如图,其中A,B,C三地在同一直线上,D点在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
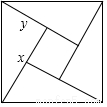 如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x、y表示直角三角形的两直角边(x>y),下列四个说法:①x2+y2=49,②x•y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )| A. | ①③ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,$\sqrt{3}$,$\sqrt{7}$ | B. | 12,16,20 | C. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | D. | 32,42,52 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com