练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．已知关于x的方程2x+a-9=0的解是x=2，则a的值为（　　）
    A．5B．4C．3D．2

    分析 把x=2代入方程，得出一个关于a的方程，求出方程的解即可．

    解答 解：把x=2代入2x+a-9=0得：4+a-9=0，
    解得：a=5，
    故选A．

    点评 本题考查了解一元一次方程，一元一次方程的解的应用，解此题的关键是能得出一个关于a的一元一次方程，难度不是很大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

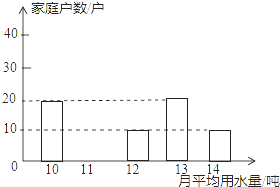    14．自来水公司对某社区600户居民家庭的用水情况做了一次调查．调查小组随机抽查了其中的100户家庭一年的月平均用电量（单位：吨），并将调查结果制成了如图所示的条形统计图．
    （1）请将条形统计图补充完整；
    （2）求这100个样本数据的平均数，众数和中位数；
    （3）根据样本数据，估计该社区600户家庭中月平均用水量不超过12吨的约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．若不等式（a-1）x＜a-1的解集是x＞1，则a的取值范围是a＜1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．若反比例函数y=$\frac{k}{x}$的图象经过点（-2，5），则y=$\frac{k}{x}$的图象在第二、四象限．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

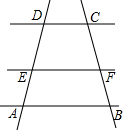    19．如图，AB∥CD，AB=a，CD=b，点E、F分别在AD、BC上，且EF∥AB，设EF到CD、AB的距离为d1、d2，则有：
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{1}$时，有EF=$\frac{a+b}{2}$；
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{2}$时，有EF=$\frac{a+2b}{3}$；
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{2}{1}$时，有EF=$\frac{2a+b}{3}$；
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{3}{1}$时，有EF=$\frac{3a+b}{4}$；
    当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{4}{1}$时，有EF=$\frac{4a+b}{5}$；当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{5}{1}$时，有EF=$\frac{5a+b}{6}$；
    （1）当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{1}{n}$时，有EF=$\frac{a+nb}{n+1}$；当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{1}$时，有EF=$\frac{ma+b}{m+1}$；（m，n均为正整数）
    （2）猜想当$\frac{{d}_{1}}{{d}_{2}}$=$\frac{m}{n}$时，有EF=$\frac{ma+nb}{m+n}$，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．某种感冒病毒的直径是0.000000712米，用科学记数法表示为7.12×10-7米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．若（x-3）0=1，则x应满足条件x≠3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．如图，若AD∥BC，则∠1=∠5，∠8=∠4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

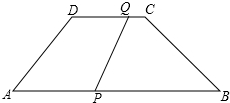    14．如图，梯形ABCD中，AB∥DC，AD=BC=5cm，AB=12cm，CD=6cm，点Q从C开始沿CD边以1cm/s的速度向D移动，同时点P从A开始沿AB以3cm/s的速度向B移动，当其中一点到达终点时运动停止．设运动时间为t秒．
    （1）当t=1.5时，求证：PQ$\stackrel{∥}{=}$AD；
    （2）当t=3s时，线段PQ能否平分对角线BD；
    （3）当t=$\frac{12}{7}$s时，点P恰好在DQ的垂直平分线上．

    查看答案和解析>>

    同步练习册答案