
 如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
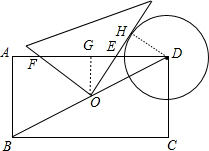 作OG⊥AD于G,连结OH,如图,
作OG⊥AD于G,连结OH,如图,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
| EO |
| EF |
| EG |
| OE |
| ||
| EF |
| ||
|
| 25 |
| 12 |
| 25 |
| 12 |


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
A、y=5-
| ||||
| B、y=10-2x(0<x<5) | ||||
C、y=5-
| ||||
D、y=10-2x(
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com